等面积法是一种常用的、重要的数学解题方法．它是利用“同一个图形的面积相等”、“分割图形后各部分的面积之和等于原图形的面积”、“同底等高或等底同高的两个三角形面积相等”等性质解决有关数学问题，在解题中，灵活运用等面积法解决相关问题，可以使解题思路清晰，解题过程简便快捷．
（1）在直角三角形中，两直角边长分别为3和4，则该直角三角形斜边上的高的长为 125125，其内切圆的半径长为 11；
（2）①如图1，P是边长为a的正△ABC内任意一点，点O为△ABC的中心，设点P到△ABC各边距离分别为h1，h2，h3，连接AP，BP，CP，由等面积法，易知12a（h1+h2+h3）=S△ABC=3S△OAB，可得h1+h2+h3=32a32a；（结果用含a的式子表示）
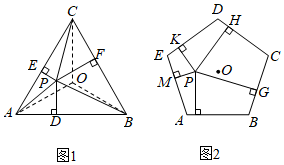
②如图2，P是边长为a的正五边形ABCDE内任意一点，设点P到五边形ABCDE各边距离分别为h1，h2，h3，h4，h5，参照①的探索过程，试用含a的式子表示h1+h2+h3+h4+h5的值．（参考数据：tan36°≈811，tan54°≈118）
（3）①如图3，已知⊙O的半径为2，点A为⊙O外一点，OA=4，AB切⊙O于点B，弦BC∥OA，连接AC，则图中阴影部分的面积为 2π32π3；（结果保留π）
②如图4，现有六边形花坛ABCDEF，由于修路等原因需将花坛进行改造，若要将花坛形状改造成五边形ABCDG，其中点G在AF的延长线上，且要保证改造前后花坛的面积不变，试确定点G的位置，并说明理由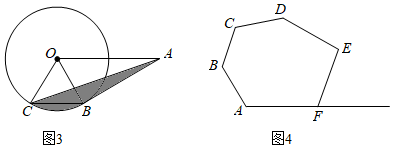
12
5
12
5
1
2
3
2
a
3
2
a
8
11
11
8
2
π
3
2
π
3
【考点】圆的综合题．
【答案】；1；；
12
5
3
2
a
2
π
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：756引用：2难度：0.1
相似题
-
1．如图，AB是圆O的直径，弦CD⊥AB于G，射线DO与直线CE相交于点E，直线DB与CE交于点H，且∠BDC=∠BCH．
（1）求证：直线CE是圆O的切线．
（2）如图1，若OG=BG，BH=1，直接写出圆O的半径；
（3）如图2，在（2）的条件下，将射线DO绕D点逆时针旋转，得射线DM，DM与AB交于点M，与圆O及切线CF分别相交于点N，F，当GM=GD时，求切线CF的长．
发布：2025/1/28 8:0:2组卷：782引用：2难度：0.1 -
2．如图，AB是圆O的直径，弦CD与AB交于点H，∠BDC=∠CBE．
（1）求证：BE是圆O的切线；
（2）若CD⊥AB，AC=2，BH=3，求劣弧BC的长；
（3）如图，若CD∥BE，作DF∥BC，满足BC=2DF，连接FH、BF，求证：FH=BF．发布：2025/1/28 8:0:2组卷：100引用：1难度：0.1 -
3．如图，AB是圆O的直径，AB=6，D是半圆ADB上的一点，C是弧BD的中点．
（1）若∠ABD=30°，求BC的长和由弦BC、BD、和弧CD围成的图形面积；
（2）若弧AD的度数是120度，在半径OB上是否存在点P，使得PC+PD的值最小，如果存在，请在备用图中画出P的位置，并求PC+PD的最小值，如果不存在，请说明理由．
发布：2025/1/28 8:0:2组卷：44引用：0难度：0.3
相关试卷
