2021-2022学年湖南省长沙市开福区青竹湖湘一外国语学校九年级（上）入学数学试卷

一、单选题（每小题4分，共32分）

• 1．下列图形中，是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：57引用：1难度：0.8

  解析

• 2．对于一组数据1，1，3，1，4，下列结论不正确的是（　　）

  A．平均数是2

  B．众数是1

  C．中位数是3

  D．方差是1.6
  组卷：449引用：8难度：0.7

  解析

• 3．函数y=

  x

  +

  2

  x

  的自变量x的取值范围是（　　）

  A．x≥-2

  B．x≥-2且x≠0

  C．x≠0

  D．x＞0且x≠-2
  组卷：1683引用：13难度：0.9

  解析

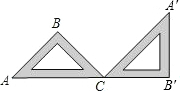• 4．如图，一块等腰直角三角形三角板ABC，在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置，使A、C、B′三点共线，那么旋转角的大小是（　　）

  A．45°

  B．90°

  C．135°

  D．180°
  组卷：111引用：3难度：0.5

  解析

• 5．如图，在菱形ABCD中，AB=5，对角线AC与BD相交于点O，且AC=6．AE⊥CD于点E，则AE的长是（　　）

  A．4

  B． 12 5

  C． 24 5

  D．5
  组卷：963引用：4难度：0.5

  解析

• 6．关于x的一元二次方程x²+mx-m-2=0的根的情况是（　　）

  A．有两个不相等的实数根

  B．有两个相等的实数根

  C．没有实数根

  D．实数根的个数由m的值确定
  组卷：2156引用：20难度：0.7

  解析

三、解答题（13，14各6分，15题8分，16，17题10分，18题12分，共52分）

• 17．已知在平面直角坐标系xOy中，抛物线C：y=ax²-5ax+c过点M（4，4）．
  （1）求c与a的关系；
  （2）当c²=25时，平移抛物线C得到新的抛物线C′，使得抛物线C′仍然过点M，并且对于C′上任意的两点T（x₁，y₁），S（x₂，y₂），当x₁＞x₂＞0时，总有

  y

  1

  -

  y

  2

  x

  1

  -

  x

  2

  ＞0，当x₂＜x₁＜0时，总有

  y

  1

  -

  y

  2

  x

  1

  -

  x

  2

  ＜0．
  ①求抛物线C′的解析式；
  ②若A，B是抛物线C′上两个不同的点，记直线AM：y=k₁x+b₁，直线BM：y=k₂x+b₂，直线AB：y=kx+b,当k₁+k₂=0时，求证：k为定值．
  组卷：232引用：1难度：0.4

  解析

• 18．如图，抛物线的开口向下，与x轴交于A，B两点（A在B左侧），与y轴交于点C．已知C（0，4），顶点D的横坐标为-

  3

  2

  ，B（1，0）．对称轴与x轴交于点E，点P是对称轴上位于顶点下方的一个动点，将线段PA绕着点P顺时针方向旋转90°得到线段PM．
  （1）求抛物线的解析式；
  （2）当点M落在抛物线上时，求点M的坐标；
  （3）连接BP并延长交抛物线于点Q，连接CQ．与对称轴交于点N．当△QPN的面积等于△QBC面积的一半时，求点Q的横坐标．
  
  组卷：396引用：4难度：0.2

  解析