北师大新版八年级上册《4.1 函数》2021年同步练习卷

一、填空题

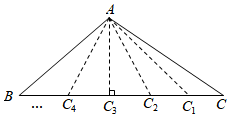• 1．如图，△ABC底边BC上的高是8cm.当三角形的顶点C沿底边所在的直线向点B运动时，三角形的面积发生变化．如果三角形的底边长为x（cm），三角形的面积为y（cm²），那么y与x的关系可以表示为

  ，其中

  是自变量，

  是因变量，

  是

  的函数．
  组卷：20引用：1难度：0.7

  解析

• 2．当x=3时，函数y=-2x+3的值是

  ．
  组卷：14引用：1难度：0.7

  解析

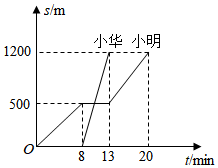• 3．小明和小华是同班同学，也是邻居，某日早晨，小明7：00先出发去学校，走了一段路后，在途中停下来吃了早饭，后来发现上学时间快到了，就跑步到学校；小华离家后直接乘公交车到了学校．如图是他们从家到学校已走的路程s（m）和小明所用时间t（min）的关系图，则下列说法中正确的是

  ．①小明吃早饭用时5min；②小华到学校的平均速度是240m/min；③小明跑步的平均速度是100m/min；④小华到学校的时间是7：05．
  组卷：521引用：6难度：0.6

  解析

• 4．嘉嘉买了6支笔花了9元钱，琪琪买了同样售价的x支笔，还买了单价为5元的三角尺两副，用y（元）表示琪琪花的总钱数，那么y与x之间的关系式应该是

  ．
  组卷：46引用：1难度：0.8

  解析

• 5．函数y=

  1

  x

  -

  1

  +

  2

  -

  x

  中自变量x的取值范围是

  ．
  组卷：94引用：4难度：0.8

  解析

• 6．某剧院的座位按下列方式设置：
  

  排数x	1	2	3	4	…
  座位数y	30	33	36	39	…

  则每排的座位数y与排数x的关系式为

  ．
  组卷：75引用：1难度：0.7

  解析

五、解答题

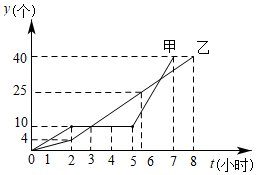• 17．某车间的甲、乙两名工人分别同时生产同种零件，在开始生产的前2个小时为生产磨合期，2个小时后有一人停工一段时间对设备进行改良升级，以提升生产效率，另一人进入正常的生产模式．他们每人生产的零件总数y（个）与生产时间t（小时）的关系如图所示．根据图象回答：
  （1）在生产过程中，哪位工人对设备进行改良升级，停止生产多少小时？
  （2）当t为多少时，甲、乙所生产的零件个数第一次相等？甲、乙中，谁先完成一天的生产任务？
  （3）设备改良升级后每小时生产零件的个数是多少？与另一工人的正常生产速度相比每小时多生产几个？
  组卷：1636引用：2难度：0.5

  解析

• 18．已知动点P以每秒2cm的速度沿图甲的边框按从B⇒C⇒D⇒E⇒F⇒A的路径移动，相应的△ABP的面积S与时间t之间的关系如图乙中的图象表示．若AB=6cm,试回答下列问题：
  
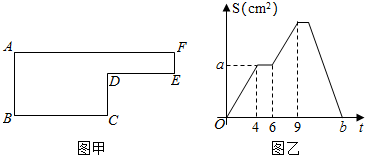
  （1）图甲中的BC长是多少？
  （2）图乙中的a是多少？
  （3）图甲中的图形面积的多少？
  （4）图乙中的b是多少？
  组卷：2153引用：24难度：0.5

  解析