2023-2024学年北京市朝阳区和平街一中八年级（上）期中数学试卷
发布：2024/10/11 10:0:1
一、选择题（共8个小题，每小题2分，共16分）下面各题均有四个选项，其中只有一个是符合题意的.
-
1．下列手机中的图标是轴对称图形的是（ ）
组卷：3013引用：47难度：0.9 -
2．下列长度的三条线段（单位：cm），能组成直角三角形的是（ ）
组卷：102引用：2难度：0.7 -
3．若一个多边形的内角和等于外角和的2倍，则这个多边形的边数为（ ）
组卷：1002引用：15难度：0.7 -
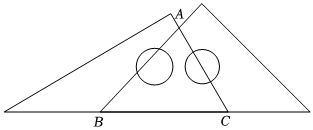4．如图，一副三角板拼成如图所示图形，则∠BAC的度数为（ ）组卷：1709引用：16难度：0.7 -
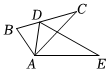5．如图，△ABC≌△ADE，∠B=80°，∠C=30°，∠DAC=35°，则∠EAC的度数为（ ）组卷：260引用：9难度：0.7 -
6．如图所示在△ABC中，AB边上的高线画法正确的是（ ）
组卷：3650引用：53难度：0.8 -
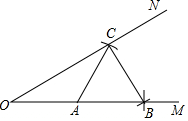7．如图，已知∠MON及其边上一点A．以点A为圆心，AO长为半径画弧，分别交OM，ON于点B和C，再以点C为圆心，AC长为半径画弧，恰好经过点B．错误的结论是（ ）组卷：837引用：14难度：0.7 -
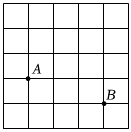8．如图，已知每个小方格的边长为1，A，B两点都在小方格的格点（顶点）上，请在图中找一个格点C，使△ABC是以AB为腰的等腰三角形，这样的格点C有（ ）组卷：2213引用：3难度：0.6
二、填空题（共8个小题，每题2分，共16分）
-
9．已知点P（-2，1），那么点P关于x轴对称的点Q的坐标是
．组卷：106引用：8难度：0.7
三、解答题（本题共68分，第17-22题，每小题5分，第23-26题，每小题5分，第27，28题，每小题5分）解答应写出文字说明，演算步骤或证明过程.
-
27．如图，过等边△ABC的顶点B在∠ABC内部作射线BP，∠ABP=α（0°＜α＜60°且α≠30°），点A关于射线BP的对称点为点D，直线CD交BP于点E，连接BD，AE．
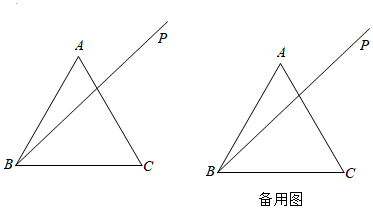
（1）依据题意，补全图形；
（2）在α（0°＜α＜60°且α≠30°）变化的过程中，∠AEB的大小是否发生变化？如果发生变化，请直接写出变化的范围；如果不发生变化，请求出∠AEB的大小；
（3）连接AD交BP于点F，用等式表示线段AE，BF，CE之间的数量关系，并给予证明．组卷：514引用：2难度：0.4 -
28．如图1，E是等边三角形ABC的边AB所在直线上一点，D是边BC所在直线上一点，且D与C不重合，若EC=ED．则称D为点C关于等边三角形ABC的反称点，点E称为反称中心．
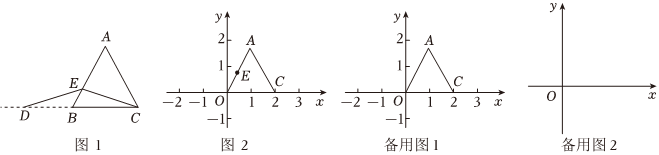
在平面直角坐标系xOy中，
（1）已知等边三角形AOC的顶点C的坐标为（2，0），点A在第一象限内，反称中心E在直线AO上，反称点D在直线OC上．
①如图2，若E为边AO的中点，在图中作出点C关于等边三角形AOC的反称点D，并直接写出点D的坐标：；
②若AE=2，求点C关于等边三角形AOC的反称点D的坐标；
（2）若等边三角形ABC的顶点为B（n,0），C（n+2，0），反称中心E在直线AB上，反称点D在直线BC上，且3≤AE＜4．请直接写出点C关于等边三角形ABC的反称点D的横坐标t的取值范围：（用含n的代数式表示）组卷：80引用：2难度：0.2
