2022-2023学年黑龙江省哈尔滨四十九中七年级（上）质检数学试卷（12月份）（五四学制）

一、选择题（每小题3分，共计30分）

• 1．下列各式是一元一次方程的是（　　）

  A．x+1

  B．3x2+1=2

  C．5x+y=3

  D．2x-1=0
  组卷：29引用：2难度：0.9

  解析

• 2．下列四个图形中，∠1和∠2是对顶角的是（　　）

  A．

  B．

  C．

  D．
  组卷：346引用：3难度：0.8

  解析

• 3．81的算术平方根是（　　）

  A．±9

  B．9

  C．±3

  D．3
  组卷：86引用：1难度：0.7

  解析

• 4．运用等式性质进行的变形，一定正确的是（　　）

  A．如果a=b,那么a+2=b-2	B．如果ac=bc,那么a=b
  C．如果 a c = b c ，那么a=b	D．如果a2=3a,那么a=3
  组卷：63引用：1难度：0.7

  解析

• 5．如图，由AD∥BC可以得到的是（　　）

  A．∠1=∠2	B．∠3+∠4=90°
  C．∠DAB+∠ABC=180°	D．∠ABC+∠BCD=180°
  组卷：745引用：5难度：0.8

  解析

• 6．如图，直角三角形ABC中，∠ACB=90°，CD⊥AB，垂足是点D，则下列说法正确的是（　　）

  A．线段AC的长表示点C到AB的距离

  B．线段CD的长表示点A到CD的距离

  C．线段BC的长表示点B到AC的距离

  D．线段BD的长表示点C到DB的距离
  组卷：496引用：5难度：0.8

  解析

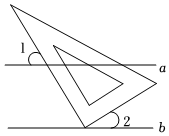• 7．如图，直角三角板的直角顶点放在直线b上，且a∥b,∠1=55°，则∠2的度数为（　　）

  A．35°

  B．45°

  C．55°

  D．25°
  组卷：1598引用：13难度：0.8

  解析

• 8．我国明代数学读本《算法统宗》一书中有这样一道题：“一支竿子一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托”，如果1托为5尺，那么索和竿子各为几尺？设竿子为x尺，可列方程为（　　）

  A．x+5- 1 2 x=5	B．x- 1 2 （x+5）=1
  C．x- 1 2 x+5=5	D．x- 1 2 （x+5）=5
  组卷：1704引用：11难度：0.6

  解析

• 9．已知点P（x,y）的坐标满足|x|=3，

  y

  =2，且xy＜0，则点P的坐标是（　　）

  A．（3，-2）

  B．（-3，2）

  C．（3，-4）

  D．（-3，4）
  组卷：982引用：6难度：0.9

  解析

三、解答题（其中21～22题各7分，23～24题各8分，25～27各10分，共计60分）

• 26．已知：AB∥CD，E、G是AB上的点，F、H是CD上的点，∠EGH=∠EFH．
  
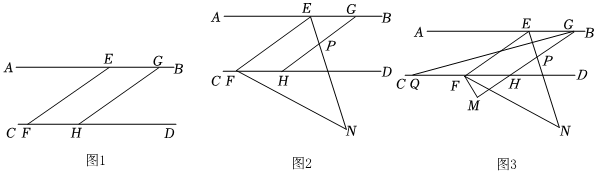
  （1）如图1，求证：EF∥GH；
  （2）如图2，EN为∠BEF的角平分线，交GH于点P，连接FN，求证：∠N=∠HPN-∠NFH；
  （3）如图3，在（2）的条件下，过点F作FM⊥GH于点M，作∠AGH的角平分线交CD于点Q，若FN平分∠DFM，且∠GQH比∠N的

  1

  3

  多3°，求∠AEF的度数．
  组卷：723引用：5难度：0.5

  解析

• 27．如图，在平面直角坐标系中，O为坐标原点，三角形ABC的边BC在x轴上，点B的坐标是（-5，0），点C在x轴的正半轴上，点A在y轴的正半轴上，它们的坐标分别为A（0，m）、C（m-1，0），且OA+OC=7，AC=5．
  
  （1）求A、C两点的坐标；
  （2）动点P从点A出发，以每秒2个单位的速度，沿射线AC运动，点P运动时间为t秒，连接OP，三角形COP的面积为S，请求出S与t之间的关系式；
  （3）在（2）的条件下，当点P在线段AC上运动时，是否存在某一时刻，使三角形COP的面积是三角形ABC面积的

  1

  8

  ，若存在，请求出t的值和P点坐标；若不存在，请说明理由．
  组卷：70引用：1难度：0.4

  解析