当前位置：试卷中心 > 试卷详情

2023-2024学年福建省泉州市南安市八年级（上）期中数学试卷

发布：2024/10/10 3:0:1

一、选择题：本题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．4的平方根是（　　）
A．2 B．-2 C．4 D．±2
组卷：264引用：75难度：0.9
解析
2．下列各数中是无理数的是（　　）
A．3.14 B．
4
C．
3
D．
22
7
组卷：59引用：4难度：0.9
解析
3．下列从左到右的变形中，是因式分解的是（　　）
A．m²-9=（m-3）² B．m²-m+1=m（m-1）
C．（m+1）²=m²+2m+1 D．m²+m=m（m+1）
组卷：82引用：2难度：0.8
解析
4．下列各式计算正确的是（　　）
A．
9
=±
3
B．
（
-
3
）
2
=
-
3
C．
3
4
=
2
D．
25
=
5
组卷：578引用：7难度：0.8
解析
5．下面的计算错误的是（　　）
A．y²•y³=y⁵ B．x⁶÷x³=x²
C．（x^m）⁵=x^5m D．（xy）⁵÷（xy）²=x³y³
组卷：56引用：2难度：0.9
解析
6．下列各式中能用平方差公式计算的是（　　）
A．（-x+2y）（x-2y） B．（1-5m）（5m-1）
C．（3x-5y）（3x+5y） D．（a+b）（-a-b）
组卷：2796引用：16难度：0.9
解析
7．单项式3a³b与单项式9a²b³的公因式是（　　）
A．3a²b B．3a³b³ C．a²b D．a³b³
组卷：892引用：5难度：0.8
解析
8．如果整式x²+mx+9恰好是一个整式的平方，那么m的值是（　　）
A．±3 B．±4.5 C．±6 D．9
组卷：803引用：13难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题：本题共9小题，共86分.解答应写出文字说明、证明过程或演算步骤.

24．我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一例．如图，这个三角形的构造法则：两腰上的数都是1，其余每个数均为其上方左右两数之和，它给出了（a+b）ⁿ（n为正整数）的展开式（按a的次数由大到小的顺序排列）的系数规律．例如，在三角形中第三行的三个数1、2、1，恰好对应（a+b）²=a²+2ab+b²展开式中的系数；第四行的四个数1、3、3、1，恰好对应着（a+b）³=a³+3a²b+3ab²+b²，展开式中的系数等等．

（1）根据上面的规律，（a+b）⁵=
；
（2）求（a+b）¹⁰展开式中各项的系数和；
（3）若今天是星期二，经过8¹⁰⁰天后是星期几．
组卷：135引用：2难度：0.5
解析
25．【知识生成】我们已经知道，通过计算几何图形的面积可以表示一些代数恒等式．例如图1可以得到（a+b）²=a²+2ab+b²，基于此，请解答下列问题：
【直接应用】（1）若
x
+
y
=
5
，xy=2，求x²+y²的值；
【类比应用】（2）若（x-3）（x-4）=1，求（x-3）²+（4-x）²的值；
以下是亮亮同学的解法：
解：∵（x-3）（x-4）=x²-7x+12=1，
∴x²-7x=-11，
∵（x-3）²+（4-x）²=x²-6x+9+16-8x+x²=2x²-14x+25，
∴（x-3）²+（4-x）²=2（x²-7x）+25=2×（-11）+25=3．
爱动脑筋的琪琪同学看了亮亮同学的解法后，灵机一动说到：“我还有其它不同的解法．”请你结合材料，类比第（1）题进行解答；
【知识迁移】（3）两块形状大小都相同的直角梯形（∠AOC=∠BCO=∠DOF=∠EFO=90°），如图2所示放置，其中A、O、F三点在同一直线上，连接AD、CF．若AF=14，每一个直角梯形的面积为69，且下底是上底的2倍，求△AOD与△COF的面积之和．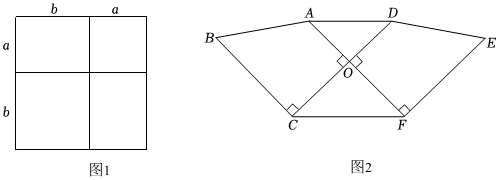
组卷：193引用：2难度：0.5
解析