2022-2023学年广东省深圳市罗湖外语学校初中部九年级（上）段考数学试卷（11月份）

一、选择题（每小题3分，共30分）

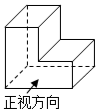• 1．如图所示的几何体的俯视图是（　　）

  A．

  B．

  C．

  D．
  组卷：350引用：5难度：0.9

  解析

• 2．在Rt△ABC中，∠C=90°，BC=4，AC=3，则sinA的值是（　　）

  A． 4 5

  B． 3 5

  C． 4 3

  D． 5 4
  组卷：223引用：1难度：0.7

  解析

• 3．对于反比例函数

  y

  =

  -

  3

  x

  ，下列说法不正确的是（　　）

  A．图象经过点（1，-3）

  B．图象分布在第二、四象限

  C．点A（x1，y1），B（x2，y2）都在反比例函数 y = - 3 x 的图象上，若x1＜x2，则y1＜y2

  D．当x＞0时，y随x的增大而增大
  组卷：157引用：2难度：0.6

  解析

• 4．如图，菱形ABCD的对角线AC，BD相交于O点，E，F分别是AB，BC边上的中点，连接EF．若EF=2

  3

  ，BD=8，则菱形ABCD的周长为（　　）

  A．8

  B．8 6

  C．16 3

  D．8 7
  组卷：222引用：8难度：0.7

  解析

• 5．下列命题，其中是真命题的是（　　）

  A．对角线互相垂直的四边形的中点四边形是菱形

  B．有一个角是直角的四边形是矩形

  C．对角线互相平分的平行四边形是菱形

  D．对角线互相垂直的矩形是正方形
  组卷：101引用：3难度：0.6

  解析

• 6．新冠肺炎是一种传染性极强的疾病，如果有一人患病，经过两轮传染后有64人患病，设每轮传染中平均一个人传染了x个人，下列列式正确的是（　　）

  A．x+x（1+x）=64	B．1+x+x2=64
  C．（1+x）2=64	D．x（1+x）=64
  组卷：1253引用：11难度：0.6

  解析

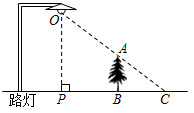• 7．如图，小树AB在路灯O的照射下形成投影BC．若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4.5m.则路灯的高度OP为（　　）

  A．3m

  B．4m

  C．4.5m

  D．5m
  组卷：2253引用：27难度：0.5

  解析

三、解答题（本大题共7小题，其中第16题6分，第17题7分，第18题6分，第19题8分，第20题8分，第21题10分，第22题10分，共55分）

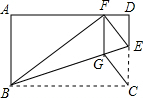• 21．如图，矩形ABCD中，点E在边CD上，将△BCE沿BE折叠，点C落在AD边上的点F处，过点F作FG∥CD交BE于点G，连接CG．
  （1）求证：四边形CEFG是菱形；
  （2）若AB=6，AD=10，求四边形CEFG的面积．
  组卷：5375引用：44难度：0.5

  解析

• 22．如图1，已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F．
  
  （1）推断：

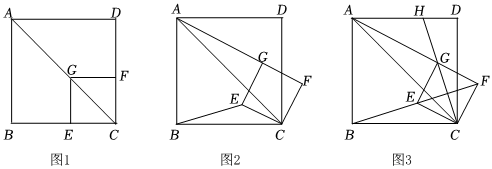
  AG

  BE

  的值为

  ；（直接写出结果）
  （2）探究与证明：将正方形CEGF绕点C顺时针方向旋转α角（0＜α＜45°），如图2所示，试探究线段AG与BE之间的数量关系，并说明理由；
  （3）拓展与运用：正方形CEGF在旋转过程中，当B，E，F三点在一条直线上时，如图3所示，延长CG交AD于点H．若AG=6，

  GH

  =

  2

  2

  ，则BC=

  ．
  组卷：230引用：2难度：0.1

  解析