当前位置：试卷中心 > 试卷详情

2023-2024学年广西南宁市邕宁区民族中学九年级（上）开学数学试卷

发布：2024/9/7 14:0:8

一、选择题（共12小题，每小题3分，共36分。在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑）

1．《北京市生活垃圾管理条例》对生活垃圾分类提出更高要求，并于2020年5月1日起施行．如图所示垃圾分类标志，是中心对称图形的是（　　）
A． B． C． D．
组卷：80引用：4难度：0.9
解析
2．下列方程中是一元二次方程的是（　　）
A．x²-
3
x
+2=0 B．xy+2=0
C．2x+2=1 D．（a²+1）x²-6=0
组卷：204引用：2难度：0.8
解析
3．抛物线y=-x²-1的图象大致是（　　）
A． B． C． D．
组卷：803引用：21难度：0.9
解析
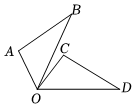4．如图，将△AOB绕着点O顺时针旋转，得到△COD，若∠AOB=40°，∠BOC=35°，则旋转角度是（　　）
A．10° B．35° C．40° D．75°
组卷：150引用：3难度：0.5
解析
5．函数①y=3x²，
②
y
=
3
2
x
2
，③y=-2x²中，图象开口大小的顺序是（　　）
A．①＞②＞③ B．①＞③＞② C．③＞②＞① D．②＞③＞①
组卷：900引用：3难度：0.5
解析
6．用配方法解方程x²=4x+1，配方后得到的方程是（　　）
A．（x-2）²=5 B．（x-2）²=4 C．（x-2）²=3 D．（x-2）²=1
组卷：229引用：14难度：0.9
解析
7．将抛物线y=x²-2x+1向上平移2个单位长度，再向左平移3个单位长度，得到抛物线y=x²+bx+c,则b,c的值为（　　）
A．b=-8，c=18 B．b=8，c=14 C．b=-4，c=6 D．b=4，c=6
组卷：584引用：7难度：0.6
解析
8．设x₁，x₂是一元二次方程x²-2x-5=0的两根，则x₁²+x₂²的值为（　　）
A．6 B．8 C．14 D．16
组卷：1453引用：17难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三.解答题（本大题共8小题，共72分，解答应写出文字说明，证明过程或演算步骤。）

25．如图（1），已知CA=CB，CD=CE，且∠ACB=∠DCE，将△DCE绕C点旋转（A、C、D三点在同一直线上除外）．
（1）求证：△ACD≌△BCE；
（2）在△DCE绕C点旋转的过程中，若ED、AB所在的直线交于点F，当点F为边AB的中点时，如图2所示．求证：∠ADF=∠BEF（提示：利用类倍长中线方法添加辅助线）；
（3）在（2）的条件下，求证：AD⊥CD．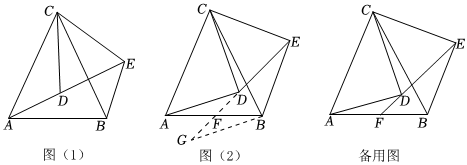
组卷：1122引用：12难度：0.3
解析
26．如图所示，在平面直角坐标系中，点B的坐标为（-3，-4），线段OB绕原点逆时针旋转后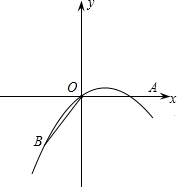与x轴的正半轴重合，点B的对应点为点A．
（1）直接写出点A的坐标，并求出经过A，O，B三点的抛物线的解析式；
（2）在抛物线的对称轴上是否存在点C，使BC+OC的值最小？若存在，求出点C的坐标，若不存在，请说明理由；
（3）如果点P是抛物线上的一个动点，且在x轴的上方，当点P运动到什么位置时，△PAB的面积最大？求出此时点P的坐标和△PAB的最大面积．
组卷：351引用：18难度：0.1
解析