当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省无锡市新吴区七年级（下）期中数学试卷

发布：2024/4/20 14:35:0

一、选择题（共10小题，共30分）

1．下列汽车商标图案中，可以由一个“基本图案”通过连续平移得到的是（　　）
A． B． C． D．
组卷：46引用：1难度：0.5
解析
2．下列运算正确的是（　　）
A．a³•a³=a⁹ B．（-2a）²=-4a²
C．（a²）⁴=a¹² D．a⁶÷a²=a⁴
组卷：170引用：5难度：0.7
解析
3．已知三角形的两边长分别为5cm和8cm,则第三边的长可以是（　　）
A．2cm B．3cm C．6cm D．13cm
组卷：1587引用：39难度：0.8
解析
4．如图，下列推理中正确的是（　　）
A．∵∠1=∠4，∴BC∥AD
B．∵∠2=∠3，∴AB∥CD
C．∵∠BCD+∠ADC=180°，∴AD∥BC
D．∵∠CBA+∠C=180°，∴BC∥AD
组卷：1322引用：14难度：0.6
解析
5．下列各式从左到右的变形中，属于因式分解的（　　）
A．x²-4y²=（x+2y）（x-2y） B．2x（x-3y）=2x²-6xy
C．（x+2）²=x²+4x+4 D．ax+bx+c=x（a+b）+c
组卷：108引用：1难度：0.8
解析
6．如图，三角板的直角顶点落在矩形纸片的一边上．若∠1=35°，则∠2的度数是（　　）
A．35° B．45° C．55° D．65°
组卷：1811引用：35难度：0.9
解析
7．如果x²+2x-2=0，那么代数式x（x+2）+3的值是（　　）
A．-5 B．5 C．3 D．-3
组卷：273引用：3难度：0.7
解析
8．已知2x+y=1，则4^x×2^y的值为（　　）
A．2 B．4 C．16 D．32
组卷：219引用：3难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题。

24．先阅读下面的内容，再解决问题：
问题：对于形如x²+2xa+a²，这样的二次三项式，可以用公式法将它分解成（x+a）²的形式．但对于二次三项式x²+2xa-3a²，就不能直接运用公式了．此时，我们可以在二次三项式x²+2xa-3a²中先加上一项a²，使它与x²+2xa的和成为一个完全平方式，再减去a²，整个式子的值不变，于是有：x²+2xa-3a²=（x²+2xa+a²）-a²-3a²=（x+a）²-4a²=（x+a）²-（2a）²=（x+3a）（x-a）像这样，先添一适当项，使式中出现完全平方式，再减去这个项，使整个式子的值不变的方法称为“配方法”．利用“配方法”，解决下列问题：
（1）分解因式：a²-6a+5；
（2）若
a
2
+
b
2
-
12
a
-
6
b
+
45
+
|
1
2
m
-
c
|
=
0
；
①当a,b,m满足条件：2^a×4^b=8^m时，求m的值；
②若△ABC的三边长是a,b,c,且c边的长为奇数，求△ABC的周长．
组卷：522引用：3难度：0.4
解析
25．概念认识
如图①，在∠ABC中，若∠ABD=∠DBE=∠EBC，则BD，BE叫做∠ABC的“三分线”．其中，BD是“邻AB三分线”，BE是“邻BC三分线”．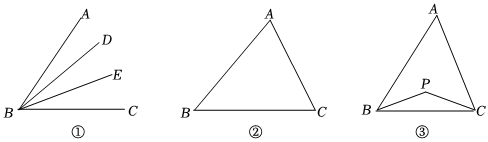

【问题解决】
（1）如图①，∠ABC=60°，BD，BE是∠ABC的“三分线”，则∠ABE=
°；
（2）如图②，在△ABC中，∠A=60°，∠B=48°，若∠B的三分线BD交AC于点D，则∠BDC=
°；
（3）如图③，在△ABC中，BP、CP分别是∠ABC邻BC三分线和∠ACB邻BC三分线，且∠BPC=140°，求∠A的度数；
（4）【延伸推广】
在△ABC中，∠ACD是△ABC的外角，∠B的三分线所在的直线与∠ACD的三分线所在的直线交于点P．若∠A=m°，∠B=n°，直接写出∠BPC的度数．（用含m、n的代数式表示）
组卷：1110引用：2难度：0.3
解析