2020-2021学年广东省广州十三中九年级（上）期中数学试卷

一、选择题（共十题：共30分）

• 1．下列图形中，不是轴对称图形，是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：345引用：16难度：0.8

  解析

• 2．下列条件中，能确定圆的是（　　）

  A．以已知点O为圆心

  B．以1cm长为半径

  C．经过已知点A，且半径为2cm

  D．以点O为圆心，1cm为半径
  组卷：750引用：10难度：0.9

  解析

• 3．平面直角坐标系内一点P（-2，3）关于原点对称的点的坐标是（　　）

  A．（3，-2）

  B．（2，3）

  C．（-2，-3）

  D．（2，-3）
  组卷：2199引用：162难度：0.9

  解析

• 4．下列关于x的一元二次方程有实数根的是（　　）

  A．x2+1=0

  B．x2+x+1=0

  C．x2-x+1=0

  D．x2-x-1=0
  组卷：962引用：118难度：0.9

  解析

• 5．青山村种的水稻2018年平均每公顷产7200kg,2020年平均每公顷产8500kg,设水稻每公顷产量的年平均增长率为x,由题意所列方程正确的是（　　）

  A．7200（1+x）2=8500

  B．7200（1+2x）=8500

  C．8500（1+x）2=7200

  D．7200+7200（1+x）+7200（1+x）2=8500
  组卷：5引用：2难度：0.6

  解析

• 6．一元二次方程3x（x-1）=2（x-1）的解是（　　）

  A． x = 2 3

  B．x=1

  C． x 1 = 1 ， x 2 = 2 3

  D．无实数根
  组卷：5引用：2难度：0.7

  解析

• 7．在函数y=（x-1）²+3中，当y随x的增大而减小时，则x的取值范围是（　　）

  A．x≥1

  B．x＞0

  C．x＜3

  D．x≤1
  组卷：583引用：3难度：0.7

  解析

• 8．某抛物线的图象向右平移2个单位再向下平移3个单位，所得图象的解析式为y=（x-1）²-4，则原抛物线的解析式为（　　）

  A．y=（x+1）2+1

  B．y=（x+1）2-1

  C．y=（x-1）2+2

  D．y=（x-1）2-2
  组卷：32引用：4难度：0.5

  解析

三、解答题（共九题：共72分）

• 24．如图1所示，在正方形ABCD中，G是CD上一点，延长BC到E，使CE=CG，
  （1）求证：△BCG≌△DCE；
  （2）将△DCE绕点D顺时针旋转90°得到△DAE′，判断四边形E′BGD是什么特殊四边形，并说明理由；
  （3）如图2所示，过点G作MN∥DE交AD于点M，交BE于点NM连接BM，设CG的长为x,正方形ABCD的边长为a（a＞0），△BMN的面积为S，试探究S与x的函数关系式，并写出x的取值范围．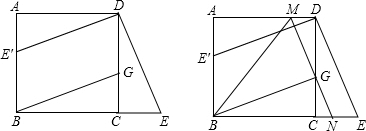
  
  组卷：78引用：2难度：0.9

  解析

• 25．如图所示，在平面直角坐标系中，点B的坐标为（-3，-4），线段OB绕原点逆时针旋转后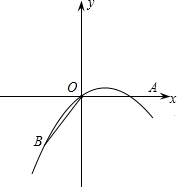与x轴的正半轴重合，点B的对应点为点A．
  （1）直接写出点A的坐标，并求出经过A，O，B三点的抛物线的解析式；
  （2）在抛物线的对称轴上是否存在点C，使BC+OC的值最小？若存在，求出点C的坐标，若不存在，请说明理由；
  （3）如果点P是抛物线上的一个动点，且在x轴的上方，当点P运动到什么位置时，△PAB的面积最大？求出此时点P的坐标和△PAB的最大面积．
  组卷：351引用：18难度：0.1

  解析