2023年浙江省宁波市中考数学适应性试卷（5月份）

一、选择题（每小题4分，共40分.在每小题给出的四个选项中，只有一项符合题目要求）

• 1．

  2

  的倒数是（　　）

  A． 2 2

  B． - 2

  C．2

  D． - 2 2
  组卷：52引用：2难度：0.9

  解析

• 2．下列计算正确的是（　　）

  A．（a3）2=a5

  B．a3•a5=a8

  C．a5+a2=a7

  D．a6÷a2=a3
  组卷：185引用：7难度：0.8

  解析

• 3．第七次全国人口普查数据显示，贵州省常住人口约为3856.21万人，将38562100用科学记数法表示为（　　）

  A．3.85621×108	B．3.85621×107
  C．0.385621×107	D．0.385621×108
  组卷：51引用：2难度：0.9

  解析

• 4．下面的几何体是由4个相同的小正方体搭成的，其中主视图与左视图相同的是（　　）

  A．

  B．B

  C．

  D．
  组卷：12引用：2难度：0.8

  解析

• 5．某校举行防疫知识竞赛，甲、乙两班的参加人数及成绩（满分100分）的平均数、中位数、方差如表所示．规定成绩大于或等于96分为优异．
  

  	参加人数	平均数	中位数	方差
  甲	40	95	93	5.1
  乙	40	95	95	3.6

  佳佳根据上述信息得出如下结论：①甲、乙两班学生成绩的平均水平相同；②甲班的成绩比乙班的成绩稳定；③乙班成绩优异的人数比甲班多；④佳佳得94分将排在甲班的前20名，其中正确的结论是（　　）

  A．①②

  B．①④

  C．③④

  D．①③④
  组卷：203引用：3难度：0.6

  解析

• 6．函数

  y

  =

  1

  x

  +

  2

  中，自变量x的取值范围是（　　）

  A．x＞-2

  B．x≥-2

  C．x≠2

  D．x≤-2
  组卷：405引用：3难度：0.8

  解析

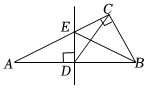• 7．如图，在△ABC中，∠ACB=90°，边AB的垂直平分线交AB于点D，交AC于点E，连接BE，CD，若BC=5，CD=6.5，则△BCE的周长为（　　）

  A．17

  B．18

  C．19

  D．20
  组卷：374引用：4难度：0.7

  解析

• 8．中国国家博物馆由原中国历史博物馆和中国革命博物馆两馆改建而成已知新馆的面积比原两馆的总面积的3倍少0.4万平方米，且新馆的面积比原两馆的总面积大4.2万平方米，设新馆的面积为x万平方米，原两馆的总面积为y万平方米，则可以列方程组（　　）

  A． x - 3 y = 0 . 4 x - y = 4 . 2	B． 3 y - x = 0 . 4 x - y = 4 . 2
  C． x - 3 y = 0 . 4 y - x = 4 . 2	D． 3 y - x = 0 . 4 y - x = 4 . 2
  组卷：495引用：5难度：0.5

  解析

三、解答题（本大题共有8小题，共80分）

• 23．（1）感知：如图1，四边形ABCD、CEFG均为正方形，试猜想线段BE和DG的数量关系为

  ．
  （2）探究：如图2，四边形ABCD、CEFG均为菱形，且∠A=∠F求证：BE=DG．
  （3）应用：如图3，四边形ABCD、CEFG均为菱形，点E在边AD上，点G在AD的延长线上，若AE=3ED，∠A=∠F，△EBC的面积为8，则菱形CEFG的面积为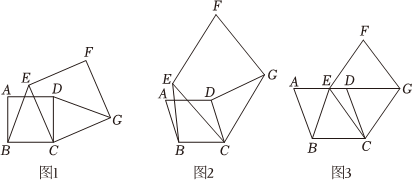

  ．
  ​
  组卷：135引用：3难度：0.2

  解析

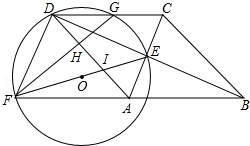• 24．如图，四边形ABCD为菱形，对角线AC，BD相交于点E，F是边BA延长线上一点，连接EF，以EF为直径作⊙O，交DC于D，G两点，AD分别与EF，GF交于I，H两点．
  （1）求∠FDE的度数；
  （2）试判断四边形FACD的形状，并证明你的结论；
  （3）当G为线段DC的中点时，
  ①求证：FD=FI；
  ②设AC=2m,BD=2n,求m：n的值．
  组卷：323引用：5难度：0.3

  解析