2022-2023学年河南省信阳市八年级（下）期中数学试卷

一、选择题（每小题3分，共30分）

• 1．若代数式

  x

  x

  -

  1

  在实数范围内有意义，则x的取值范围为（　　）

  A．x＞0

  B．x≥0

  C．x≠0

  D．x≥0且x≠1
  组卷：2195引用：21难度：0.9

  解析

• 2．下列运算正确的是（　　）

  A．2 3 × 3 3 =6 3

  B． 2 + 3 = 5

  C．5 5 -2 2 =3 3

  D． 2 ÷ 3 = 6 3
  组卷：78引用：2难度：0.5

  解析

• 3．菱形具有而矩形不一定具有的特征是（　　）

  A．对角相等

  B．对角线互相平分

  C．一组对边平行，另一组对边相等

  D．对角线互相垂直
  组卷：138引用：5难度：0.9

  解析

• 4．若点A（-2，m）在正比例函数y=-

  1

  2

  x的图象上，则m的值是（　　）

  A． 1 4

  B．- 1 4

  C．1

  D．-1
  组卷：1006引用：70难度：0.9

  解析

• 5．若△ABC的三边a,b,c满足（a-b）（a²+b²-c²）=0，则△ABC是（　　）

  A．等腰三角形

  B．等边三角形

  C．等腰直角三角形

  D．等腰三角形或直角三角形
  组卷：238引用：3难度：0.6

  解析

• 6．如图，在菱形ABCD中，∠A=110°，E，F分别是边AB和BC的中点，EP⊥CD于点P，则∠FPC=（　　）

  A．35°

  B．45°

  C．50°

  D．55°
  组卷：2727引用：73难度：0.7

  解析

• 7．已知一次函数y=2x-3经过哪几个象限（　　）

  A．一、二、三

  B．一、三、四

  C．一、二、四

  D．二、三、四
  组卷：358引用：7难度：0.7

  解析

三、解答题（本大题共8小题，共75分）

• 21．某工厂现有甲种原料360千克，乙种原料290千克，计划利用这两种原料生产A、B两种产品共50件．已知生产一件A种产品，需用甲种原料9千克、乙种原料3千克，可获利润700元；生产一件B种产品，需用甲种原料4千克、乙种原料10千克，可获利润1200元．设生产A种产品的生产件数为x,A、B两种产品所获总利润为y（元）．
  （1）试写出y与x之间的函数关系式；
  （2）求出自变量x的取值范围；
  （3）利用函数的性质说明哪种生产方案获总利润最大？最大利润是多少？
  组卷：980引用：12难度：0.5

  解析

• 22．（1）感知：如图1，四边形ABCD、CEFG均为正方形，试猜想线段BE和DG的数量关系为

  ．
  （2）探究：如图2，四边形ABCD、CEFG均为菱形，且∠A=∠F求证：BE=DG．
  （3）应用：如图3，四边形ABCD、CEFG均为菱形，点E在边AD上，点G在AD的延长线上，若AE=3ED，∠A=∠F，△EBC的面积为8，则菱形CEFG的面积为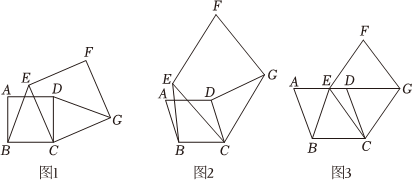

  ．
  ​
  组卷：135引用：3难度：0.2

  解析