2022-2023学年浙江省杭州市下城区安吉路实验学校八年级（上）期中数学试卷

一、选择题：本大是有10个小题，每小题3分。共30分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．下列各点中，在第二象限的点是（　　）

  A．（-3，2）

  B．（-3，-2）

  C．（3，2）

  D．（3，-2）
  组卷：476引用：16难度：0.9

  解析

• 2．由下列长度的三条线段不能组成三角形的是（　　）

  A．2cm,3cm,4cm	B．2cm,2cm,3cm
  C．2cm,2cm,4cm	D．3cm,3cm,4cm
  组卷：22引用：3难度：0.7

  解析

• 3．一个等腰三角形的顶角等于50°，则这个等腰三角形的底角度数是（　　）

  A．50°

  B．65°

  C．75°

  D．130°
  组卷：223引用：8难度：0.9

  解析

• 4．要说明命题“两个无理数的和是无理数”是假命题，可选择的反例是（　　）

  A．2， 2

  B． 2 ， 2

  C． 2 ， 3

  D． 2 ， - 2
  组卷：22引用：2难度：0.8

  解析

• 5．一个三角形三个内角的度数之比为2：3：6，则这个三角形一定是（　　）

  A．等腰三角形

  B．直角三角形

  C．锐角三角形

  D．钝角三角形
  组卷：175引用：4难度：0.9

  解析

• 6．已知实数a,b满足a+1＞b-1，则（　　）

  A．a＞b

  B．b＞a

  C．a＞b+1

  D．a+3＞b+1
  组卷：23引用：2难度：0.8

  解析

• 7．关于一次函数y=-3x+1，下列说法正确的是（　　）

  A．图象过点（-1，3）

  B．y随x的增大而增大

  C．图象经过第一、二、三象限

  D．与y轴的交点坐标为（0，1）
  组卷：1728引用：13难度：0.7

  解析

三、解答题：本大题有7个小题，共66分，解答应写出文字说明、证明过程或演算步骤．

• 22．一次函数y₁=kx+b（k,b是常数，k≠0）和y₂=x+2的图象交于点A．
  （1）若点A在x轴上，求

  b

  k

  的值．
  （2）若点A（2，m），当x＞2时，y₁＞y₂，直接写出k的取值范围．
  （3）若k+b＜0，点Q（5，m²+1）在一次函数y₁=kx+b图象上，求证：k＞0．
  组卷：84引用：2难度：0.6

  解析

• 23．已知，DA，DB，BC是从点D出发的三条线段，且DA=DB=DC．
  
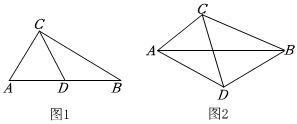
  （1）如图1，若点D在线段AB，连接AC，BC，试判断△ABC形状，并说明理由．
  （2）如图2，连接AC，BC，AB，且AB与CD相交于点E．①若AC=BC，AB=16，DC=10，求线段AC的长．②求证：∠BDC=2∠BAC．
  组卷：104引用：1难度：0.2

  解析