当前位置：试卷中心 > 试卷详情

2023-2024学年山东省青岛市市北区滨海学校八年级（上）月考数学试卷（10月份）

发布：2024/8/31 14:0:8

1．下列实数是无理数的是（　　）
A．
3
8
B．
2
3
C．
π
2
D．|-3|
组卷：42引用：5难度：0.7
解析
2．我国是最早了解勾股定理的国家之一，下面四幅图中，不能证明勾股定理的是（　　）
A． B． C． D．
组卷：1477引用：12难度：0.4
解析
3．点A（x,y）的坐标满足y=0，则点A在（　　）
A．原点 B．x轴上 C．y轴上 D．x轴或y轴上
组卷：264引用：2难度：0.9
解析
4．下列运算结果错误的是（　　）
A．
（
-
2
）
2
=
2
B．
（
-
2
）
2
=
2
C．
4
=±2 D．
3
-
8
=-2
组卷：228引用：4难度：0.8
解析
5．如图是在方格纸上画出的小旗图案，若用（0，0）表示点A，（0，4）表示点B，那么点C的位置可表示为（　　）
A．（0，3） B．（2，3） C．（3，0） D．（3，2）
组卷：414引用：4难度：0.9
解析
6．“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成一个大正方形，设直角三角形较长直角边长为a,较短直角边长为b,若ab=24，大正方形的面积为129，则小正方形的边长为（　　）
A．9 B．10 C．11 D．12
组卷：589引用：7难度：0.5
解析

18．如图所示，某住宅社区在相邻两楼之间修建一个上方是一个半圆，下方是长方形的仿古通道，现有一辆卡车装满家具后，高4米，宽2.8米，求这辆送家具的卡车能否通过这个通道．
组卷：326引用：1难度：0.5
解析
19．综合与实践．
积累经验
（1）我们在第十二章《全等三角形》中学习了全等三角形的性质和判定，在一些探究题中经常用以上知识转化角和边，进而解决问题．例如：我们在解决：“如图1，在△ABC中，∠ACB=90°，AC=BC，线段DE经过点C，且AD⊥DE于点D，BE⊥DE于点E．求证：AD=CE，CD=BE”这个问题时，只要证明△ADC≌△CEB，即可得到解决，请写出证明过程；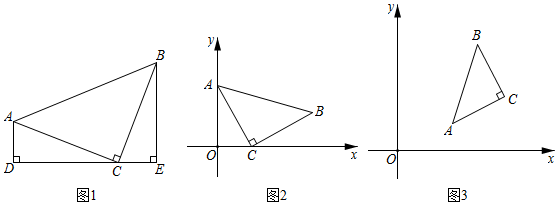

类比应用
（2）如图2，在平面直角坐标系中，△ABC中，∠ACB=90°，AC=BC，点A的坐标为（0，2），点C的坐标为（1，0），求点B的坐标．
拓展提升
（3）如图3，△ABC在平面直角坐标系中，∠ACB=90°，AC=BC，点A的坐标为（2，1），点C的坐标为（4，2），则点B的坐标为
．
组卷：626引用：10难度：0.4
解析