当前位置：试卷中心 > 试卷详情

2023-2024学年湖南省长沙市天心区湘郡培粹中学九年级（上）第一次作业精练数学试卷

发布：2024/9/8 11:0:12

一.选择题（共10小题，每小题3分共30分）

1．随着我国航天领域的快速发展，从“天宫一号”发射升空，到天和核心舱归位，我国正式迈入了“空间站时代”．下面是有关我国航天领域的图标，其图标既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
组卷：374引用：18难度：0.9
解析
2．2022年10月16日上午10时，中国共产党第二十次全国代表大会开幕，习近平代表第十九届中央委员会向党的二十大作报告，报告中提到，十年来，我国人均国内生产总值从三万九千八百元增加到八万一千元，八万一千用科学记数法可以表示为（　　）
A．0.81×10⁵ B．8.1×10³ C．81×10³ D．8.1×10⁴
组卷：328引用：9难度：0.8
解析
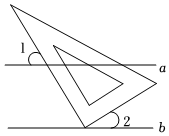3．如图，直角三角板的直角顶点放在直线b上，且a∥b,∠1=55°，则∠2的度数为（　　）
A．35° B．45° C．55° D．25°
组卷：1598引用：13难度：0.8
解析
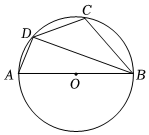4．如图，四边形ABCD内接于⊙O，AB是⊙O的直径，∠ABD=20°，则∠BCD的度数是（　　）
A．90° B．100° C．110° D．120°
组卷：2105引用：13难度：0.5
解析
5．如图，点B，F，E，D共线，∠B=∠D，BE=DF，添加一个条件，不能判定△ABF≌△CDE的是（　　）
A．AF∥CE B．∠A=∠C C．AF=CE D．AB=CD
组卷：955引用：20难度：0.8
解析
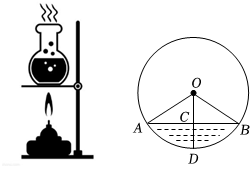6．如图，一个底部呈球形的烧瓶，球的半径为5cm,瓶内液体的最大深度CD=2cm,则截面圆中弦AB的长为（　　）cm.
A．4
2
B．6 C．8 D．8.4
组卷：972引用：9难度：0.6
解析
7．我国南宋数学家杨辉在《田亩比类乘除捷法》中记录了这样的一个问题：“直田积八百六十四步，只云长阔共六十步，问长多阔几何？”其大意是：矩形面积是864平方步，其中长与宽和为60步，问长比宽多多少步？若设长比宽多x步，则下列符合题意的方程是（　　）
A．（60-x）x=864 B．
60
-
x
2
•
60
+
x
2
=
864
C．（60+x）x=864 D．（30+x）（30-x）=864
组卷：1615引用：26难度：0.8
解析
8．若A（-
1
2
，y₁），B（1，y₂），C（2，y₃）三点都在二次函数y=-（x-2）²+h的图象上，则y₁，y₂，y₃的大小关系为（　　）
A．y₁＜y₂＜y₃ B．y₁＜y₃＜y₂ C．y₃＜y₁＜y₂ D．y₃＜y₂＜y₁
组卷：1201引用：9难度：0.4
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三.解答题（共9小题，第17、18、19题各6分，第20、21题各8分，第22、23题各9分，第24、25题各10分，共72分）

24．已知两个函数，如果对于任意的自变量x,这两个函数对应的函数值记为y₁，y₂，都有点（x,y₁）、（x,y₂）关于点（x,x）对称，则称这两个函数为关于y=x的对称函数，例如，
y
1
=
1
2
x
和
y
2
=
3
2
x
为关于y=x的对称函数．
（1）判断：①y₁=3x和y₂=-x；②y₁=x+1和y₂=x-1；③
y
1
=
x
2
+
1
和
y
2
=
x
2
-
1
，其中为关于y=x的对称函数的是
（填序号）；
（2）若y₁=3x+2和y₂=kx+b（k≠0）为关于y=x的对称函数．求k、b的值．
（3）若
y
1
=
a
x
2
+
bx
+
c
（
a
≠
0
）
和
y
2
=
x
2
+
n
为关于y=x的对称函数，令w=y₂-y₁，当函数w与函数y=x（0≤x≤2）有且只有一个交点时，求n的取值范围．
组卷：612引用：3难度：0.5
解析
25．在平面直角坐标系中，抛物线y=x²-2x-3与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C．

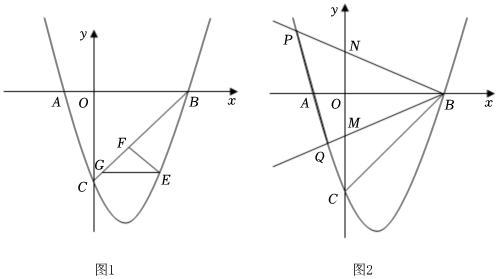
（1）求A，B，C三点的坐标；
（2）如图1，连接BC，点E是第四象限内抛物线上的动点，过点E作EF⊥BC于点F，EG∥x轴交直线BC于点G，求△EFG面积的最大值；
（3）如图2，点M在线段OC上（点M不与点O重合），点M、N关于原点对称，射线BN、BM分别与抛物线交于P、Q两点，连接PA、QA，若△BMN的面积为S₁，四边形BPAQ的面积为S₂，求
S
1
S
2
的值．
组卷：1031引用：12难度：0.2
解析