1．（2024秋•镇海区校级期中）我们把纵坐标和横坐标都是整数的点称为整点．函数y=x²-2ax+a²+2a+1和y=x+3所围成的封闭图形（不包含边界）共有4个整点，则a的取值范围是（　　）

2．（2024秋•南岗区校级月考）如图1，在平面直角坐标系中，点B在x轴负半轴上，点A在第二象限，连接AO、AB，OC⊥AB，∠ABO=2∠AOC．
（1）求证：△AOB为等腰三角形；
（2）如图2，点D从A出发以每秒1个单位长度沿BA延长线运动，运动时间为t,点Q为OA上一点，连接DQ并延长交OB于点E，若DQ=EQ，设OE长度为d,请用含t的式子表示d；
（3）在（2）的条件下，点F在x轴正半轴上，连接FQ，点H在FQ上，连接DH，若∠ABO=60°，且2∠QFB+∠QDH+∠QEF=180°，FH=DQ，点W在QE延长线上，连接FW，且FW=FQ，过点W作WG⊥x轴于点G，若G（-11.9，0），且BG-OF=1，求此时t的值．

3．我们来研究下面的表格问题：在4×4的方格表中放入8个棋子，如果每行每列恰有2个棋子，共有多少种放置方法？可以发现，对一种放置方法交换两行或交换两列，以及一系列的这样操作，就可以得到别的放置方法．
（1）考虑如图1的放置方法，通过交换行列的一系列变换，可以得到多少不同的放置方法？
（2）类似地，如图2的放置方法，通过交换行列的一系列变换，可以得到多少不同的放置方法？
（3）证明：任何放置方法都能通过一系列行列交换变为（1）、（2）两种情况之一，由此给出所有的放置方案数．

4．（2023春•沙坪坝区校级期末）对于一个四位自然数，若其各个数位上的数字都不为0，且千位数字与百位数字的差为2，个位数字与十位数字的差也为2，则称这样的四位数为“内差数”．设一个“内差数”M=1000a+100b+10c+d（3≤a≤9，1≤b≤7，1≤c≤7，3≤d≤9，且a,b,c,d均为整数），将M的千位数字与个位数字对调，百位数字与十位数字对调得到新数M′．对于一个四位自然数N，分别按顺序取N的千位数字与百位数字组成两位数，百位数字与十位数字组成两位数，十位数字与个位数字组成两位数，将3个两位数之和记为F（N），例如N=1234，则F（N）=12+23+34=69．若（k为整数），且F（M）+F（M′）-2能被5整除，则所有满足条件的“内差数”M的和为 ．

5．（2024春•柯城区校级期中）如图，▱ABCD的对角线AC，BD交于点O，设．
（1）若，∠ADC=45°．则▱ABCD的面积为 ．
（2）若AE平分∠BAD，交BC边于点E，连结OE．设，则n与k满足的关系式为 ．

6．（2024•高新区模拟）对于平面直角坐标系xOy中的图形M和图形N，给出如下定义：P为图形M上任意一点，Q为图形N上任意一点，如果P，Q两点间的距离有最小值，则称这个最小值为图形M，N间的“捷径距离”，记为d（图形M，图形N）．已知△ABC三个顶点的坐标分别为A（-2，1），B（-3，2），C（-1，2），将三角形ABC绕点D（a,a）逆时针旋转90°得到△A′B′C′，若△A′B′C′上任意点都在半径为4的⊙O内部或圆上，则△ABC与△A′B′C′的“捷径距离”d（△ABC，△A′B′C′）的最小值是 ，最大值是 ．

7．（2024•西安校级四模）（1）如图①，在四边形ABCD中，∠BAD=∠BCD=90°，AC和BD是两条对角线，∠ABD=30°，过点A作AC的垂线交CD的延长线于点E．求的值．
（2）炎热的夏天即将到来，水上乐园成为亲子游玩的好去处．某开发公司将在一片浅水湖建造一个大型的水上乐园，并同时开发三条水上商业步行街．如图②，四边形ABCD是项目开发的雏形图，其中A，B，D是三条步行街的入口．AC，BC，DC分别是通向水上乐园C的三条步行街（三条街道宽度相同）．根据仪器测量BD的长约千米，∠ABD=30°，∠ADB=45°．同时根据设计要求还要满足∠BCD=75°．由于招商类型与环境设计的不同，预计AC段每月平均每千米的租金收入是10万元，BC段每月平均每千米的租金收入是万元，CD段每月平均每千米的租金收入是20万元．问是否存在一点C，使得三条步行街每月的租金总收入最大．若存在，求出每月租金总收入的最大值，若不存在，请说明理由．

8．（2024•长沙模拟）阅读材料，回答下列小题．
阅读材料1：
调和是射影几何重要不变量交比的一种特殊形式，早在古希腊，数学家们便发现了一组具有特殊比例关系的点列：调和点列．
我们定义：若一直线上依次存在四点A，B，C，D，满足AB•CD=BC•AD，则称A，B，C，D为调和点列．从直线外一点P引射线PA，PB，PC，PD，则称PA，PB，PC，PD为调和线束．
（1）如图1，过圆Q外一点P作圆Q的切线PA，PB，并引圆Ω的割线PCD，设PD与A交于点E．
①求证：P，C，E，D是调和点列．
②求证：AC•BD=BC•AD．
阅读材料2：阿波罗尼斯圆：对于平面上的两定点A，B和平面上一动点P，若P到A和B的距离之比为定值，则点P的轨迹是一个圆，我们称该圆是点P关于AB的“阿氏圆”．
（2）根据阅读材料1，2，回答①②小题．（本题图未给出）
①证明阿波罗尼斯圆，并确定该圆圆心的位置．
②若点P关于AB的“阿氏圆”交AB于C，D，求证：A，C，B，D为调和点列．
（3）如图2，ABCD是平行四边形，G是三角形ABD的重心，点P，Q在直线BD上，满足GP与PC垂直，GQ与QC垂直．求证：AG平分∠PAQ．

9．（2023秋•甘井子区期中）问题情境：
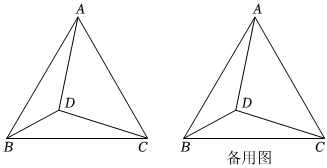
课堂上老师提出如下问题：如图，在等边△ABC内有任意一点D，连接DA，DB，DC，将等边△ABC分成三个小三角形．请利用三角板，将△BDC以点B为旋转中心，逆时针旋转60°，画出旋转后的图形．

数学思考：
（1）请你按要求在图1中完成画图．
（2）老师又给出了一组具体的数值，DB=1，DC=2，，要求同学们求∠BDC的度数．请你利用在图1中画出的图形，完成解答．
深入探究：
（1）“智慧小组”的同学发现，D点的位置不是唯一确定的，DB，DC，DA的长度只要满足一定的关系，∠BDC的度数可以同上题②中的结论一样．请你写出三者之间应满足的关系：（直接写出答案）
（2）“创新小组”的同学在“智慧小组”发现的基础上，又提出了新问题，并经过探索做出了猜想，得到了老师的肯定．
新问题：设等边三角形的边长为4，当∠BDC 的度数是多少时，D点就是唯一存在的呢？
探索过程：研究了将△BDC以点B为旋转中心，顺时针旋转60°所得到的图形．
猜想：当DA+DB+DC的值最小时，可以求出∠BDC的度数，此时D点就是唯一的．