当前位置：试卷中心 > 试卷详情

2024年河南省洛阳市中考数学二模试卷

发布：2025/11/26 10:0:11

一、选择题（每小题3分，共30分）下列各小题均有四个选项，其中只有一个是正确的。

1．在实数1，0，-1，-
1
2
中，最小的实数是（　　）
A．-
1
2
B．-1 C．1 D．0
组卷：17引用：2难度：0.7
2．在同一平面内，不重合的三条直线a、b、c中，如果a⊥b,b⊥c,那么a与c的位置关系是（　　）
A．垂直 B．平行 C．相交 D．不能确定
组卷：203引用：8难度：0.6
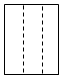3．下列各选项中，其主视图如图所示的是（　　）
A． B． C． D．
组卷：824引用：6难度：0.7
4．某组女生占全组人数的
1
3
，再加上5名女生后就占全组人数的一半，设原来全组有x名同学，则可列方程为（　　）
A．
1
3
x
+
5
=
1
2
B．
1
3
x
+
5
=
1
2
x
C．
1
3
x
+
5
=
1
2
（
x
+
5
）
D．
1
3
x
=
1
2
（
x
+
5
）
组卷：62引用：2难度：0.9
5．若关于x的方程kx²-x+4=0有实数根，则k的取值范围是（　　）
A．k≤16 B．k≤
1
16
C．k≤16，且k≠0 D．k≤
1
16
，且k≠0
组卷：2049引用：6难度：0.5
6．如图，在菱形ABCD中，对角线AC与BD交于点O，OE⊥AB，垂足为E，若∠ADC=130°，则∠AOE的大小为（　　）
A．75° B．65° C．55° D．50°
组卷：2082引用：66难度：0.9
7．如图，在四边形ABCD中，AD∥BC，AB=CD，B=60°，AD=2，BC=8，点P从点B出发沿折线BA-AD-DC匀速运动，同时，点Q从点B出发沿折线BC-CD匀速运动，点P与点Q的速度相同，当二者相遇时，运动停止，设点P运动的路程为x,△BPQ的面积为y,则y关于x的函数图象大致是（　　）
A． B．
C． D．
组卷：1141引用：9难度：0.1
8．不等式组
x
+
2
＞
0
4
-
2
x
≤
0
的解集在数轴上表示正确的是（　　）
A． B．
C． D．
组卷：86引用：3难度：0.5
9．下列等式中，正确的是（　　）
A．3a+2b=5ab B．2（a-b）=2a-b
C．（a+b）²=a²+b² D．（-2a³）²=4a⁶
组卷：14引用：2难度：0.7
10．温州有轨交通S₂线总投资约21 600 000 000元，数据21 600 000 000用科学记数法可表示为（　　）
A．0.216×10¹¹ B．2.16×10¹⁰ C．21.6×10⁹ D．216×10⁸
组卷：117引用：2难度：0.8

二、填空题（每小题3分，共15分）

11．如果y=
2
x
-
3
+
3
-
2
x
+
2
，则2x+y=
．
组卷：802引用：10难度：0.7
12．甲、乙两超市（大型商场）同时开业，为了吸引顾客，都举行有奖酬宾活动：凡购物满100元，均可得到一次摸奖的机会．在一个纸盒里装有2个红球和2个白球，除颜色外其它都相同，摸奖者一次从中摸出两个球，根据球的颜色决定送礼金券（在他们超市使用时，与人民币等值）的多少（如下表）．
甲超市：
球两红一红一白两白
礼金券（元） 5 10 5
乙超市：
球两红一红一白两白
礼金券（元） 10 5 10
如果只考虑中奖因素，你将会选择去

超市购物．请说明理由

．
组卷：45引用：1难度：0.7
13．已知
1
x
-
1
y
=
3
，则代数式
2
x
-
14
xy
-
2
y
x
-
2
xy
-
y
的值为

．
组卷：1802引用：99难度：0.7
14．如图所示，若△ABC内一点P满足∠PAC=∠PBA=∠PCB，则点P为△ABC的布洛卡点，三角形的布洛卡点是法国数学家长数学教育家克洛尔于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡重新发现，并用他的名字命名．问题：已知在等腰直角三角形DEF中，∠EDF=90°，若点Q为△DEF的布洛卡点，DQ=1，则EQ+FQ=
．
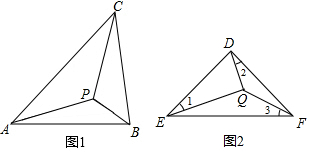组卷：344引用：2难度：0.4
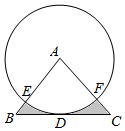15．如图所示，在△ABC中，BC=4，以点A为圆心，2为半径的⊙A与BC相切于点D，交AB于点E，交AC于点F，且∠EAF=80°，则图中阴影部分的面积是
．
组卷：73引用：67难度：0.9

三、解答题（本大题共8小题，共75分）

16．某民航飞机在大连海域失事，为调查失事原因，决定派海军潜水员打捞飞机上的黑匣子，如图所示，一潜水员在A处以每小时8海里的速度向正东方向划行，在A处测得黑匣子B在北偏东60°的方向，划行半小时后到达C处，测得黑匣子B在北偏东30°的方向，在潜水员继续向东划行多少小时，距离黑匣子B最近，并求最近距离．
组卷：134引用：24难度：0.3
17．矩形ABCD中，AF、CE分别平分∠BAD，∠BCD，并交线段BC，AD于点F，E．当动点P从点A匀速运动到点F时，动点Q恰好从点C匀速运动到点B．记AP=x,BQ=y,且y与x满足关系式：y=-
5
2
4
x+10．
（1）判断AF与CE的位置关系，并说明理由．
（2）求AF，CF的长度．
（3）①当PQ平行于△ECD的一边时，求所有满足条件的x的值．
②连接DB，对角线DB交PQ于点O，若点O恰好为PQ的三等分点，请直接写出x的值．
组卷：45引用：1难度：0.3
18．如图1，抛物线y=ax²+bx-3（a≠0）与x轴分别交于点A（-1，0）和点B（3，0），与y轴交于点C，连接AC，BC．

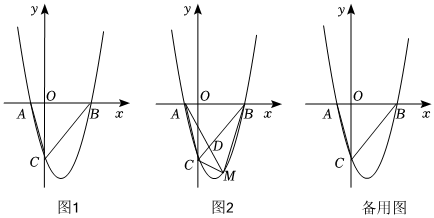
（1）求抛物线的解析式．
（2）如图2，M为线段BC下方抛物线上一动点，连接AM，BM和CM，线段AM和BC交于点D．设△BCM的面积为S₁，△ACM的面积为S₂，且S=S₁-S₂．当S最大时，求点M的坐标．
（3）在（2）的条件下，过点M作y轴的平行线交x轴于点N，P是直线MN上的一点，Q是直线MN右侧抛物线上的一点，当△BPQ为等边三角形时，请直接写出点Q的坐标．
组卷：115引用：2难度：0.2
19．某移动通讯公司开设了两种通讯业务．“全球通”使用者要缴50元月租费，然后每通话1min,再付话费0.4元；“快捷通”不缴月租费，每通话1min,付话费0.6元，若一个月内通话x min,两种费用分别为y₁元和y₂元．
（1）写出y₁、y₂与x之间的函数关系式；
（2）某人估计一个月内通话200min,应选择哪种通讯业务合算些？
组卷：28引用：1难度：0.5
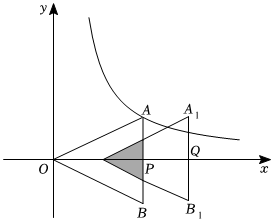20．如图，Rt△OAB中，OA=OB，AB⊥x轴于点P，点B的坐标为（2，-1）．反比例函数
y
=
k
x
（x＞0）的图象经过点A．
（1）求k的值；
（2）将△OAB沿x轴向右平移1个单位长度至ΔO₁A₁B₁处，求反比例函数的图象与A₁B₁的交点Q的坐标；
（3）直接写出阴影部分的面积．
组卷：45引用：1难度：0.5
21．如图，画出下列多边形的对角线．
组卷：13引用：1难度：0.5

22．今年八月，世界人民期待已久的东京奥运会成功举办，我国运动健儿们在奥运赛场上取得了十分优异
的成绩．随着夏季奥运会的结束，人们将迎来2022年北京冬奥会．毛泽东同志曾说“德志皆寄予于体，
无体是无德志也“，某社区为了加强社区居民对冬奥会的了解，通过网络宣传冬奥会知识，并鼓励社区
居民在线参与作答《2022年北京冬奥会知识点》模拟试卷，社区管理员随机从甲、乙两个小区各抽取
20名人员的答卷成绩，并对他们的成绩（单位：分）进行统计、分析，过程如下：
收集数据
甲小区：85 80 95 100 90 95 85 65 75 85 89 90 70 90 100 80 80 90 96 75
乙小区：80 60 80 95 65 100 90 85 85 80 95 75 80 90 70 80 95 75 100 90
整理数据

成绩x（分） 60≤x≤70 70＜x≤80 80＜x≤90 90＜x≤100

甲小区 2 5 a b

乙小区 3 7 5 5

分析数据

统计量平均数中位数众数

甲小区 85.75 87.5 c

乙小区 83.5 d 80

应用数据
（1）填空：a=
，b=
，c=
，d=
；
（2）若甲小区共有600人参与答卷，请估计甲小区成绩大于80分的人数；
（3）社区管理员看完统计数据，认为甲小区对冬奥会知识掌握更好，请你写出社区管理员的理由．

组卷：72引用：1难度：0.6

23．（1）解方程：1-
7
+
3
x
8
=
3
x
-
10
4
-x
（2）[（-3）³+2^-3×（-8^-1）^-2×（-
1
2
）^-3×（2013-π）⁰
（3）利用平方差公式进行计算：40
1
3
×39
2
3
组卷：46引用：1难度：0.8

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A． 1 3 x + 5 = 1 2	B． 1 3 x + 5 = 1 2 x
C． 1 3 x + 5 = 1 2 （ x + 5 ）	D． 1 3 x = 1 2 （ x + 5 ）

A．k≤16	B．k≤ 1 16
C．k≤16，且k≠0	D．k≤ 1 16 ，且k≠0

A．3a+2b=5ab	B．2（a-b）=2a-b
C．（a+b）²=a²+b²	D．（-2a³）²=4a⁶

成绩x（分）	60≤x≤70	70＜x≤80	80＜x≤90	90＜x≤100
甲小区	2	5	a	b
乙小区	3	7	5	5

统计量	平均数	中位数	众数
甲小区	85.75	87.5	c
乙小区	83.5	d	80

球	两红	一红一白	两白
礼金券（元）	5	10	5

球	两红	一红一白	两白
礼金券（元）	10	5	10

2024年河南省洛阳市中考数学二模试卷

一、选择题（每小题3分，共30分）下列各小题均有四个选项，其中只有一个是正确的。

1．在实数1，0，-1，-12中，最小的实数是（ ）

2．在同一平面内，不重合的三条直线a、b、c中，如果a⊥b,b⊥c,那么a与c的位置关系是（ ）

3．下列各选项中，其主视图如图所示的是（ ）

4．某组女生占全组人数的13，再加上5名女生后就占全组人数的一半，设原来全组有x名同学，则可列方程为（ ）

5．若关于x的方程kx2-x+4=0有实数根，则k的取值范围是（ ）

6．如图，在菱形ABCD中，对角线AC与BD交于点O，OE⊥AB，垂足为E，若∠ADC=130°，则∠AOE的大小为（ ）

8．不等式组x+2＞04-2x≤0的解集在数轴上表示正确的是（ ）

9．下列等式中，正确的是（ ）

10．温州有轨交通S2线总投资约21 600 000 000元，数据21 600 000 000用科学记数法可表示为（ ）

二、填空题（每小题3分，共15分）

11．如果y=2x-3+3-2x+2，则2x+y=．

13．已知1x-1y=3，则代数式2x-14xy-2yx-2xy-y的值为 ．

15．如图所示，在△ABC中，BC=4，以点A为圆心，2为半径的⊙A与BC相切于点D，交AB于点E，交AC于点F，且∠EAF=80°，则图中阴影部分的面积是 ．

三、解答题（本大题共8小题，共75分）

21．如图，画出下列多边形的对角线．

23．（1）解方程：1-7+3x8=3x-104-x（2）[（-3）3+2-3×（-8-1）-2×（-12）-3×（2013-π）0（3）利用平方差公式进行计算：4013×3923

1．在实数1，0，-1，-
1
2
中，最小的实数是（　　）

2．在同一平面内，不重合的三条直线a、b、c中，如果a⊥b,b⊥c,那么a与c的位置关系是（　　）

3．下列各选项中，其主视图如图所示的是（　　）

4．某组女生占全组人数的
1
3
，再加上5名女生后就占全组人数的一半，设原来全组有x名同学，则可列方程为（　　）

5．若关于x的方程kx²-x+4=0有实数根，则k的取值范围是（　　）

6．如图，在菱形ABCD中，对角线AC与BD交于点O，OE⊥AB，垂足为E，若∠ADC=130°，则∠AOE的大小为（　　）

8．不等式组
x
+
2
＞
0
4
-
2
x
≤
0
的解集在数轴上表示正确的是（　　）

9．下列等式中，正确的是（　　）

10．温州有轨交通S₂线总投资约21 600 000 000元，数据21 600 000 000用科学记数法可表示为（　　）

11．如果y=
2
x
-
3
+
3
-
2
x
+
2
，则2x+y=
．

13．已知
1
x
-
1
y
=
3
，则代数式
2
x
-
14
xy
-
2
y
x
-
2
xy
-
y
的值为

．

15．如图所示，在△ABC中，BC=4，以点A为圆心，2为半径的⊙A与BC相切于点D，交AB于点E，交AC于点F，且∠EAF=80°，则图中阴影部分的面积是
．

23．（1）解方程：1-
7
+
3
x
8
=
3
x
-
10
4
-x
（2）[（-3）³+2^-3×（-8^-1）^-2×（-
1
2
）^-3×（2013-π）⁰
（3）利用平方差公式进行计算：40
1
3
×39
2
3