当前位置：试卷中心 > 试卷详情

2023年贵州省统一命题中考数学模拟试卷

发布：2025/11/26 10:0:11

一、选择题：以下每小题均有A、B、C、D四个选项，其中只有一个选项正确，请用2B铅笔在答题卡相应位置作答，每小题3分，共36分。

1．若m+n=0，则m,n的取值一定是（　　）
A．都是0 B．至少有一个等于0
C．互为相反数 D．m是正数，n是负数
组卷：131引用：2难度：0.9
2．如图，从A地到B地有三条路线，由上至下依次记为路线a、b、c,则从A地到B地的最短路线是c,其中蕴含的数学道理是（　　）
A．两点确定一条直线 B．两点之间，线段最短
C．经过一点有无数条直线 D．直线比曲线短
组卷：843引用：9难度：0.9
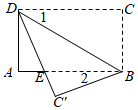3．如图，将矩形纸片ABCD沿BD折叠，得到△BC′D，C′D与AB交于点E，若∠1=40°，则∠2的度数为（　　）
A．25° B．20° C．15° D．10°
组卷：1240引用：8难度：0.6
4．在平面直角坐标系内有一点P，已知点P到x轴的距离为2，到y轴的距离为4，则点P的坐标不可能是（　　）
A．（-2，-4） B．（4，2） C．（-4，2） D．（4，-2）
组卷：371引用：6难度：0.7
5．如图，在x轴，y轴上分别截取OA，OB，使OA=OB，再分别以点A，B为圆心，以大于
1
2
AB长为半径画弧，两弧交于点P．若点P的坐标为（a,2a-3），则a的值为（　　）
A．3 B．4 C．5 D．6
组卷：461引用：7难度：0.6
6．2023年2月，中国旅游研究院发布的《中国旅游经济蓝皮书》预测，2023年我国国内旅游人数将达到45.5亿人次，同比增长约73%，恢复到2019年的76%；实现国内旅游收入约4万亿元，同比增长约89%，恢复到2019年的71%．将45.5亿用科学记数法表示应为（　　）
A．455×10⁷ B．45.5×10⁸ C．4.55×10⁹ D．0.455×10¹⁰
组卷：88引用：4难度：0.9
7．在雨地里放置一个无盖的容器，如果雨水均匀地落入容器，容器水面高度h与时间t的函数图象如图所示，那么这个容器的形状可能是（　　）
A． B． C． D．
组卷：697引用：4难度：0.9
8．如图，将一刻度尺放在数轴上．

①若刻度尺上0cm和4cm对应数轴上的点表示的数分别为1和5，则1cm对应数轴上的点表示的数是2；
②若刻度尺上0cm和4cm对应数轴上的点表示的数分别为1和9，则1cm对应数轴上的点表示的数是3；
③若刻度尺上0cm和4cm对应数轴上的点表示的数分别为-2和2，则1cm对应数轴上的点表示的数是-1；
④若刻度尺上0cm和4cm对应数轴上的点表示的数分别为-1和1，则1cm对应数轴上的点表示的数是-0.5．
上述结论中，所有正确结论的序号是（　　）
A．①② B．②④ C．①②③ D．①②③④
组卷：802引用：10难度：0.7
9．如图是小李书桌上放的一本书，则这本书的俯视图是（　　）
A． B． C． D．
组卷：485引用：64难度：0.9
10．若关于x的一元二次方程kx²+2x-1=0有实数根，则k的取值范围是（　　）
A．k＞-1 B．k≥-1 C．k＞-1且k≠0 D．k≥-1且k≠0
组卷：1007引用：71难度：0.9
11．如图，在▱ABCD中，EF∥AB，DE：EA=2：3，EF=4，则CD的长为（　　）
A．
16
3
B．8 C．10 D．16
组卷：1491引用：33难度：0.9
12．一组数据：3，4，4，4，5．若拿掉一个数据4，则发生变化的统计量是（　　）
A．极差 B．方差 C．中位数 D．众数
组卷：171引用：6难度：0.7

二、填空题：每题4分，共16分，

13．如图所示，四边形ABCD中，AC⊥BD于点O，AO=CO=4，BO=DO=3，点P为线段AC上的一个动点．过点P分别作PM⊥AD于点M，作PN⊥DC于点N．连接PB，在点P运动过程中，PM+PN+PB的最小值等于
．
组卷：3393引用：19难度：0.5
14．点A（a,b）、B（a-1，c）均在函数
y
=
1
x
的图象上．若a＜0，则b
c（填“＞”、“＜”或”=”）．
组卷：147引用：9难度：0.9
15．当x=

时，分式
x
2
-
x
-
2
x
-
2
的值为0．
组卷：37引用：1难度：0.5
16．张明想给单位打电话，可电话号码中的一个数字记不清楚了，只记得6352□87，张明在□的位置上随意选了一个数字补上，恰好是单位电话号码的概率是

．
组卷：71引用：64难度：0.7

三、解答题：本大题共9题，共计98分，解答应写出必要的文字说明、证明过程或演算步骤.

17．甲、乙两人同时从相距90千米的A地前往B地，甲乘汽车，乙骑电动车，甲到达B地停留半个小时后返回A地，如图是他们与A地之间的距离y（千米）与经过的时间x（小时）之间的函数关系图象．
（1）求甲从B地返回A地的过程中，y与x之间的函数关系式，并写出自变量x的取值范围；
（2）已知乙骑电动车的速度为40千米/小时，求乙出发后多少小时和甲相遇？
组卷：612引用：1难度：0.3
18．如图，建筑物CD的高为35米，从C点测得A点的仰角α为53°，从A点测得D点的俯角β为37°，求建筑物AB的高度和两座建筑物间的水平距离BC．（参考数据sin37°≈
3
5
，cos37°≈
4
5
，tan37°≈
3
4
，sin53°≈
4
5
，cos53°≈
3
5
，tan53°≈
4
3
）
组卷：369引用：2难度：0.5
19．已知，AC和BD为⊙O的两条弦，并且AB²+CD²=4R²，其中R为⊙O的半径．求证：AC⊥BD．
组卷：139引用：1难度：0.1
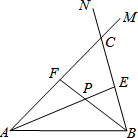20．在线段AB的同侧作射线AM和BN，若∠MAB与∠NBA的平分线分别交射线BN，AM于点E，F，AE和BF交于点P．如图，点点同学发现当射线AM，BN交于点C；且∠ACB=60°时，有以下两个结论：
①∠APB=120°；②AF+BE=AB．
那么，当AM∥BN时：
（1）点点发现的结论还成立吗？若成立，请给予证明；若不成立，请求出∠APB的度数，写出AF，BE，AB长度之间的等量关系，并给予证明；
（2）设点Q为线段AE上一点，QB=5，若AF+BE=16，四边形ABEF的面积为32
3
，求AQ的长．
组卷：2349引用：4难度：0.1
21．解不等式组
3
-
x
＞
1
-
x
+
1
4
①
7
x
+
1
≥
5
（
x
-
1
）
②
，并把解集在数轴上表示出来．
组卷：74引用：7难度：0.7
22．如图，一次函数y=-x+4的图象与反比例函数y=
k
x
（k为常数，且k≠0）的图象交于A（1，a），B（3，b）两点．
（1）求反比例函数的表达式；
（2）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标；
（3）求△PAB的面积．
组卷：551引用：4难度：0.3
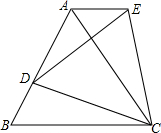23．如图，△ABC是等边三角形，D是AB边上一点，以CD为边作等边△CDE，使点E、A在直线DC的同侧，连接AE，判断AE与BC的位置关系，并说明理由．
组卷：202引用：3难度：0.1
24．某市团委在2015年3月初组成了300个学雷锋小组，现从中随机抽取6个小组在3月份做好事件数的统计情况如图所示：

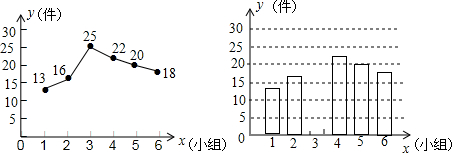
（1）这6个学雷锋小组在2015年3月份共做好事多少件？
（2）补全条形统计图；
（3）请估计该市300个学雷锋小组在2015年3月份共做好事多少件？
组卷：774引用：56难度：0.5
25．已知：二次函数y=x²+px+q,当x=1时，y=4；当x=2时，y=-5．
（1）求这个二次函数的解析式．
（2）求这个二次函数的顶点坐标和对称轴．
组卷：383引用：1难度：0.7

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．都是0	B．至少有一个等于0
C．互为相反数	D．m是正数，n是负数

A．两点确定一条直线	B．两点之间，线段最短
C．经过一点有无数条直线	D．直线比曲线短

2023年贵州省统一命题中考数学模拟试卷

一、选择题：以下每小题均有A、B、C、D四个选项，其中只有一个选项正确，请用2B铅笔在答题卡相应位置作答，每小题3分，共36分。

1．若m+n=0，则m,n的取值一定是（ ）

2．如图，从A地到B地有三条路线，由上至下依次记为路线a、b、c,则从A地到B地的最短路线是c,其中蕴含的数学道理是（ ）

3．如图，将矩形纸片ABCD沿BD折叠，得到△BC′D，C′D与AB交于点E，若∠1=40°，则∠2的度数为（ ）

4．在平面直角坐标系内有一点P，已知点P到x轴的距离为2，到y轴的距离为4，则点P的坐标不可能是（ ）

5．如图，在x轴，y轴上分别截取OA，OB，使OA=OB，再分别以点A，B为圆心，以大于12AB长为半径画弧，两弧交于点P．若点P的坐标为（a,2a-3），则a的值为（ ）

7．在雨地里放置一个无盖的容器，如果雨水均匀地落入容器，容器水面高度h与时间t的函数图象如图所示，那么这个容器的形状可能是（ ）

9．如图是小李书桌上放的一本书，则这本书的俯视图是（ ）

10．若关于x的一元二次方程kx2+2x-1=0有实数根，则k的取值范围是（ ）

11．如图，在▱ABCD中，EF∥AB，DE：EA=2：3，EF=4，则CD的长为（ ）

12．一组数据：3，4，4，4，5．若拿掉一个数据4，则发生变化的统计量是（ ）

二、填空题：每题4分，共16分，

13．如图所示，四边形ABCD中，AC⊥BD于点O，AO=CO=4，BO=DO=3，点P为线段AC上的一个动点．过点P分别作PM⊥AD于点M，作PN⊥DC于点N．连接PB，在点P运动过程中，PM+PN+PB的最小值等于 ．

14．点A（a,b）、B（a-1，c）均在函数y=1x的图象上．若a＜0，则b c（填“＞”、“＜”或”=”）．

15．当x= 时，分式x2-x-2x-2的值为0．

16．张明想给单位打电话，可电话号码中的一个数字记不清楚了，只记得6352□87，张明在□的位置上随意选了一个数字补上，恰好是单位电话号码的概率是 ．

三、解答题：本大题共9题，共计98分，解答应写出必要的文字说明、证明过程或演算步骤.

18．如图，建筑物CD的高为35米，从C点测得A点的仰角α为53°，从A点测得D点的俯角β为37°，求建筑物AB的高度和两座建筑物间的水平距离BC．（参考数据sin37°≈35，cos37°≈45，tan37°≈34，sin53°≈45，cos53°≈35，tan53°≈43）

19．已知，AC和BD为⊙O的两条弦，并且AB2+CD2=4R2，其中R为⊙O的半径．求证：AC⊥BD．

21．解不等式组3-x＞1-x+14①7x+1≥5（x-1）②，并把解集在数轴上表示出来．

22．如图，一次函数y=-x+4的图象与反比例函数y=kx（k为常数，且k≠0）的图象交于A（1，a），B（3，b）两点．（1）求反比例函数的表达式；（2）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标；（3）求△PAB的面积．

23．如图，△ABC是等边三角形，D是AB边上一点，以CD为边作等边△CDE，使点E、A在直线DC的同侧，连接AE，判断AE与BC的位置关系，并说明理由．

25．已知：二次函数y=x2+px+q,当x=1时，y=4；当x=2时，y=-5．（1）求这个二次函数的解析式．（2）求这个二次函数的顶点坐标和对称轴．

1．若m+n=0，则m,n的取值一定是（　　）

2．如图，从A地到B地有三条路线，由上至下依次记为路线a、b、c,则从A地到B地的最短路线是c,其中蕴含的数学道理是（　　）

3．如图，将矩形纸片ABCD沿BD折叠，得到△BC′D，C′D与AB交于点E，若∠1=40°，则∠2的度数为（　　）

4．在平面直角坐标系内有一点P，已知点P到x轴的距离为2，到y轴的距离为4，则点P的坐标不可能是（　　）

5．如图，在x轴，y轴上分别截取OA，OB，使OA=OB，再分别以点A，B为圆心，以大于
1
2
AB长为半径画弧，两弧交于点P．若点P的坐标为（a,2a-3），则a的值为（　　）

7．在雨地里放置一个无盖的容器，如果雨水均匀地落入容器，容器水面高度h与时间t的函数图象如图所示，那么这个容器的形状可能是（　　）

9．如图是小李书桌上放的一本书，则这本书的俯视图是（　　）

10．若关于x的一元二次方程kx²+2x-1=0有实数根，则k的取值范围是（　　）

11．如图，在▱ABCD中，EF∥AB，DE：EA=2：3，EF=4，则CD的长为（　　）

12．一组数据：3，4，4，4，5．若拿掉一个数据4，则发生变化的统计量是（　　）

13．如图所示，四边形ABCD中，AC⊥BD于点O，AO=CO=4，BO=DO=3，点P为线段AC上的一个动点．过点P分别作PM⊥AD于点M，作PN⊥DC于点N．连接PB，在点P运动过程中，PM+PN+PB的最小值等于
．

14．点A（a,b）、B（a-1，c）均在函数
y
=
1
x
的图象上．若a＜0，则b
c（填“＞”、“＜”或”=”）．

15．当x=

时，分式
x
2
-
x
-
2
x
-
2
的值为0．

16．张明想给单位打电话，可电话号码中的一个数字记不清楚了，只记得6352□87，张明在□的位置上随意选了一个数字补上，恰好是单位电话号码的概率是

．

19．已知，AC和BD为⊙O的两条弦，并且AB²+CD²=4R²，其中R为⊙O的半径．求证：AC⊥BD．

21．解不等式组
3
-
x
＞
1
-
x
+
1
4
①
7
x
+
1
≥
5
（
x
-
1
）
②
，并把解集在数轴上表示出来．

25．已知：二次函数y=x²+px+q,当x=1时，y=4；当x=2时，y=-5．
（1）求这个二次函数的解析式．
（2）求这个二次函数的顶点坐标和对称轴．