当前位置：试卷中心 > 试卷详情

2022年湖南省株洲市芦淞区中考数学模拟试卷

发布：2025/11/26 10:0:11

一.选择题（本题共10小题，每小题4分，共40分）

1．从-2，-1，-
1
2
，1，2这五个数中，随机抽取一个数，记为a,若数a使关于x的不等式组
2
x
+
7
≥
9
x
-
a
＜
0
无解，且使分式方程
a
2
x
-
3
+
a
-
2
2
x
-
3
=-1的解为正分数，那么这五个数中所有满足条件的a的值之和是（　　）
A．-3 B．-
5
2
C．-2 D．-
7
2
组卷：223引用：2难度：0.9
2．下列几何体中，俯视图与主视图完全相同的几何体是（　　）
A．圆锥 B．球 C．三棱柱 D．四棱锥
组卷：90引用：3难度：0.8
3．小米在用尺规作图作△ABC边AC上的高BH，作法如下：
①分别以点D，E为圆心，大于
1
2
DE的长为半径作弧，两弧交于F；
②作射线BF，交边AC于点H；
③以B为圆心，BK长为半径作弧，交直线AC于点D和E；
④取一点K，使K和B在AC的两侧；
所以，BH就是所求作的高．
其中顺序正确的作图步骤是（　　）
A．①②③④ B．④③②① C．②④③① D．④③①②
组卷：482引用：9难度：0.7
4．计算-27÷3×
1
3
的结果是（　　）
A．-27 B．27 C．-3 D．3
组卷：141引用：3难度：0.9
5．两条对角线相等且互相垂直平分的四边形是（　　）
A．平行四边形 B．矩形 C．菱形 D．正方形
组卷：1225引用：25难度：0.9
6．若（a+3b）²=11，a-3b=4，则ab的值是（　　）
A．
-
9
4
B．
7
12
C．
-
5
12
D．
9
4
组卷：968引用：3难度：0.8
7．在一次15人参加的歌唱比赛中，预赛成绩各不同要取前8名参加决赛杨超越已经知道自己的成绩，她想知道自己是否能进入决赛，只需要再知道这15名选手成绩的（　　）
A．平均数 B．众数 C．方差 D．中位数
组卷：231引用：4难度：0.7
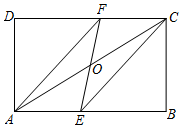8．如图，已知点O是矩形ABCD的对称中心，且AB＞AD．点E从点A出发沿AB向点B运动，移动到点B停止，延长EO交CD于点F，则四边形AECF的形状不可能是（　　）
A．平行四边形 B．正方形 C．矩形 D．菱形
组卷：200引用：5难度：0.5
9．二次函数y=（x-a）（x-b）-2（a＜b）与x轴的两个交点的横坐标分别为m和n,且m＜n,下列结论正确的是（　　）
A．m＜a＜n＜b B．a＜m＜b＜n C．m＜a＜b＜n D．a＜m＜n＜b
组卷：4737引用：21难度：0.5
10．光的速度约是30万千米/秒，这个速度用科学记数法表示是为（　　）
A．3×10⁵ 米/秒 B．0.3×10⁶ 米/秒
C．30×10⁷ 米/秒 D．3×10⁸ 米/秒
组卷：16引用：2难度：0.9

二.填空题（本题共8小题，每小题4分，共32分）

11．大围山野外滑雪场是拥有一定倾斜度的高级道、专业练习道．有一段雪道的垂直高度约为200米，它的坡度为i=1：3，那么这段雪道长约为
米（结果保留根号）．
组卷：192引用：2难度：0.6
12．分解因式：-3x²+27y²=

．
组卷：54引用：1难度：0.7
13．计算：
27
-
1
3
+（3-π）⁰=
．
组卷：56引用：1难度：0.7
14．如图，正方形ABCD对角线相交于点O，CP⊥DP于P，CP=5，DP=7，则△POD面积为
．
组卷：926引用：3难度：0.4
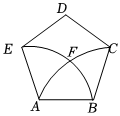15．如图，在正五边形ABCDE中，分别以点A，B为圆心，AB长为半径画弧，两弧交于点F，若AB=6．则弧EF的长为
．
组卷：71引用：2难度：0.5
16．如果反比例函数y=
k
x
的图象经过点（1，3），那么它一定经过点（-1，

）．
组卷：319引用：5难度：0.7
17．如图，四边形ABCD中，若去掉一个60°的角得到一个五边形，则∠1+∠2=
度．
组卷：2010引用：35难度：0.7
18．一个不透明的口袋中有5个完全相同的小球，把它们分别标号为1，2，3，4，5，随机提取一个小球，则取出的小球标号是奇数的概率是
．
组卷：460引用：63难度：0.7

三.解答题（本大题共8小题，共78分）

19．计算：
ta
n
2
45
°
-
2
cos
60
°
+
（
2
-
π
）
0
-
（
-
1
2
）
-
1
．
组卷：726引用：6难度：0.5
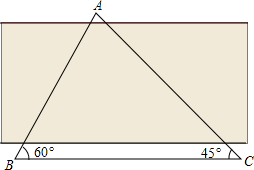20．如图，为了测量黄河某一段河流宽度，在河北选了一点A，在河南岸相距200m的B、C两点，分别测得∠ABC=60°，∠ACB=45°，求这段河流的宽度．
组卷：39引用：1难度：0.3
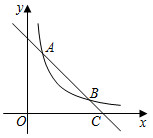21．如图，已知反比例函数y₁=
k
1
x
的图象与一次函数y₂=k₂x+b的图象在第一象限交于A（1，3），B（3，m）两点，一次函数的图象与x轴交于点C．
（1）求反比例函数和一次函数的表达式；
（2）当x为何值时，y₂＞0？
（3）已知点P（0，a）（a＞0），过点P作x轴的平行线，在第一象限内交一次函数y₂=k₂x+b的图象于点M，交反比例函数y₁=
k
1
x
的图象于点N．结合函数图象直接写出当PM＞PN时a的取值范围．
组卷：257引用：2难度：0.3
22．先化简，再求代数式
x
x
+
2
-
x
2
+
2
x
+
1
x
+
2
÷
x
2
-
1
x
-
1
的值，其中x=
2
-2．
组卷：197引用：1难度：0.1
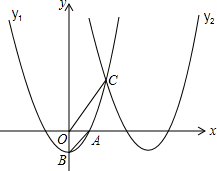23．如图，抛物线y₁=x²-1交x轴的正半轴于点A，交y轴于点B，将此抛物线向右平移4个单位得抛物线y₂，两条抛物线相交于点C．
（1）请直接写出抛物线y₂的解析式；
（2）若点P是x轴上一动点，且满足∠CPA=∠OBA，求出所有满足条件的P点坐标；
（3）在第四象限内抛物线y₂上，是否存在点Q，使得△QOC中OC边上的高h有最大值？若存在，请求出点Q的坐标及h的最大值；若不存在，请说明理由．
组卷：882引用：56难度：0.1
24．在一个不透明的口袋中放入4个白球和16个红球，它们除颜色外完全相同．
（1）求从口袋中随机摸出一个球是白球的概率；
（2）现从口袋中取出若干个红球，并放入相同数量的白球，充分摇匀后，要使从口袋中随机摸出一个球是白球的概率是
3
5
，问取出了多少个红球？
组卷：197引用：2难度：0.7
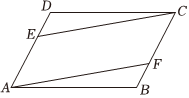25．如图，在平行四边形ABCD中，E、F分别是边AD、BC的一点，且DE=BF，连接AF、CE．求证：四边形AFCE是平行四边形．
组卷：421引用：10难度：0.5
26．如图，▱ABCD中，AE⊥BC，AF⊥CD，E，F分别是垂足．求证：
AB
BC
=
AE
AF
．
组卷：45引用：2难度：0.6