当前位置：试卷中心 > 试卷详情

2022年黑龙江省哈尔滨市南岗区松雷中学中考数学模拟试卷

发布：2025/11/26 10:0:11

一、选择题（每小题3分，共30分）

1．将二次函数y=x²+bx+c的图象先向左平移3个单位长度，再向上平移2个单位长度得到二次函数y=x²-2x+1的图象，则b,c的值分别是（　　）
A．b=14，c=-8 B．b=-2，c=4 C．b=-8，c=14 D．b=4，c=-2
组卷：266引用：3难度：0.8
2．已知a,b,c为非零的实数，且不全为正数，则
a
|
a
|
+
ab
|
ab
|
+
ac
|
ac
|
+
bc
|
bc
|
的所有可能结果的绝对值之和等于（　　）
A．4 B．6 C．8 D．10
组卷：546引用：2难度：0.7
3．分式方程
2
x
-
1
-1=0的解是（　　）
A．x=1 B．x=-2 C．x=3 D．x=-3
组卷：525引用：10难度：0.6
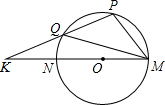4．如图，MN是半圆O的直径，K是MN延长线上一点，直线KP交半圆于点Q，P．若∠K=20°，∠PMQ=40°，则∠MQP等于（　　）
A．30° B．35° C．40° D．50°
组卷：310引用：1难度：0.9
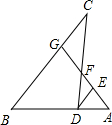5．如图，点G、F分别是△BCD的边BC、CD上的点，BD的延长线与GF的延长线相交于点A，DE∥BC交GA于点E，则下列结论错误的是（　　）
A．
AD
BD
=
AE
EG
B．
DE
CG
=
DF
CF
C．
AE
AG
=
DE
BC
D．
AD
AB
=
DE
BG
组卷：4339引用：45难度：0.9
6．下列图形中，对称轴条数最多的是（　　）
A． B． C． D．
组卷：16引用：3难度：0.9
7．如图，平面直角坐标系中，点A，B的坐标分别为（-1，2），（-1，0），将△OAB绕点O顺时针旋转90°得到△OA₁B₁，点A₁恰好落在反比例函数y=
k
x
的图象上，则k的值是（　　）
A．
1
2
B．-
1
2
C．2 D．-2
组卷：128引用：1难度：0.5
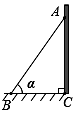8．如图，一架长2.5米的梯子AB斜靠在墙上，已知梯子底端B到墙角C的距离为1.5米，设梯子与地面所夹的锐角为α，则cosα的值为（　　）
A．
3
5
B．
4
5
C．
3
4
D．
4
3
组卷：206引用：2难度：0.7
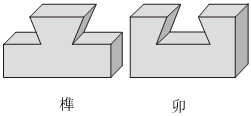9．在我国古代建筑中经常使用榫卯构件，如图是某种榫卯构件的示意图，其中卯的俯视图是（　　）
A． B． C． D．
组卷：1530引用：23难度：0.7
10．已知a,b为实数，且满足ab＞0，a+b-2=0，当a-b为整数时，ab的值为（　　）
A．
3
4
或
1
2
B．
1
4
或1 C．
3
4
或1 D．
1
4
或
3
4
组卷：1004引用：7难度：0.6

二、填空题（每小题3分，共30分）

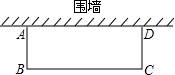11．如图，邻边不等的矩形花圃ABCD，它的一边AD利用已有的围墙，另外三边所围的栅栏的总长度是6m.若矩形的面积为4m²，则AB的长度是
m（可利用的围墙长度超过6m）．
组卷：1304引用：46难度：0.5
12．计算2
3
2
-
54
的结果是

．
组卷：182引用：4难度：0.5
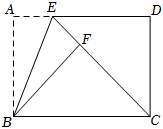13．如图，长方形ABCD中，∠A=∠ABC=∠BCD=∠D=90°，AB=CD=3，AD=BC=5，点E为射线AD上的一个动点，△ABE与△FBE关于直线BE对称，当点E、F、C三点共线时，AE的长为
．
组卷：902引用：2难度：0.4
14．把多项式2a²-4ab+2b²分解因式的结果是

．
组卷：181引用：37难度：0.9
15．如图，AB为⊙O的直径，CD为⊙O的弦，∠ACD=25°40′，则∠BAD的度数为

．
组卷：122引用：2难度：0.5
16．已知扇形的圆心角为120°，所对的弧长为
8
π
3
，则此扇形的面积是
．
组卷：909引用：58难度：0.7
17．在函数y=
3
x
2
x
+
4
中，自变量x的取值范围是

．
组卷：163引用：66难度：0.7
18．如图，平面直角坐标系xOy中，点A（2，0），以OA为半径作⊙O，若点P，B都在⊙O上，且四边形AOPB为菱形，则点P的坐标为
．
组卷：77引用：6难度：0.7
19．某市高新技术产业产值突破110亿元，数据“110亿”用科学记数法可表示为
．
组卷：56引用：1难度：0.5
20．若实数a关于x的不等式组
x
3
+
1
≥
x
+
3
2
x
-
1
≥
a
+
x
2
有解且最多3个整数解，则符合条件的a的取值范围是
．
组卷：316引用：2难度：0.6

三、解答题：（21-22每题7分，23-24每题8分，25-27每题10分，共计60分）

21．对于点P和图形G，若在图形G上存在不重合的点M和点N，使得点P关于线段MN中点的对称点在图形G上，则称点P是图形G的“中称点”．在平面直角坐标系xOy中，已知点A（1，0），B（1，1），C（0，1）．
（1）在点P₁（
1
2
，0），P₂（
1
2
，
1
2
），P₃（1，-2），P₄（-1，2）中，
是正方形OABC的“中称点”；
（2）⊙T的圆心在x轴上，半径为1．
①当圆心T与原点O重合时，若直线y=x+m上存在⊙T的“中称点”，求m的取值范围；
②若正方形OABC的“中称点”都是⊙T的“中称点”，直接写出圆心T的横坐标t的取值范围．
组卷：706引用：4难度：0.1
22．电信部门要修建一座电视信号发射塔，如图所示，按照设计要求，发射塔到两个城镇A，B的距离相等，到两条高速公路OM和ON的距离也必须相等，发射塔应建在什么位置？在图上标出它的位置．
组卷：23引用：2难度：0.5
23．如图，AD是△ABC的中线，AE∥BC，BE交AD于点F，交AC于G，F是AD的中点．
（1）求证：四边形ADCE是为平行四边形；
（2）若EB是∠AEC的角平分线，请写出图中所有与AE相等的边．
组卷：2780引用：5难度：0.1
24．先化简，再求值：
a
a
-
2
÷（
a
a
-
2
-
4
a
a
2
-
4
），其中a=
2
+2．
组卷：2342引用：13难度：0.6
25．在建党100周年之际，某校对全校学生进行了一次党史知识测试，成绩评定共分为A，B，C，D四个等级，随机抽取了部分学生的成绩讲行调查，将获得的数据绘制成两幅不完整的统计图．

根据统计图提供的信息，解答下列问题：
（1）在这次调查中一共抽取了
名学生；
（2）请补全条形统计图；
（3）扇形统计图中，D等级对应的圆心角度数是
度；
（4）根据抽样调查的结果，请你估计该校2000名学生中有多少名学生的成绩评定为C等级．
组卷：615引用：12难度：0.7
26．周末小明陪爸爸去陶瓷商城购买一些茶壶和一些茶杯，了解情况后发现甲、乙两家商店都在出售两种同样品牌的茶壶和茶杯，定价相同，茶壶每把定价30元，茶杯每把定价5元，且两家都有优惠．甲商店买一送一大酬宾（买一把茶壶送一只茶杯）；乙商店全场九折优惠．小明的爸爸需茶壶5把，茶杯若干只（不少于5只）．
（1）设购买茶杯a只，若在甲商店购买，需付
元钱；若在乙店购买，需付
元钱．（均用含a的代数式表示并化简）
（2）根据前面问题的解答，当购买茶杯超过20只时，猜想应该到
商店购买比较合算？（请直接写出结论，不用说明理由．）
（3）当购买茶杯多少只时，两家商店付款一样？为什么？
组卷：89引用：2难度：0.1
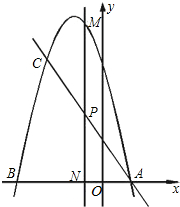27．如图，抛物线y=a（x+3）（x-1）与x轴相交于A、B两点（点A在点B右侧），过点A的直线交抛物线于另一点C，点C的坐标为（-2，6）．
（1）求a的值及直线AC的函数关系式；
（2）P是线段AC上一动点，过点P作y轴的平行线，交抛物线于点M，交x轴于点N．
①求线段PM长度的最大值；
②在抛物线上是否存在这样的点M，使得△CMP与△APN相似？如果存在，请直接写出所有满足条件的点M的坐标（不必写解答过程）；如果不存在，请说明理由．
组卷：453引用：19难度：0.5

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

2022年黑龙江省哈尔滨市南岗区松雷中学中考数学模拟试卷

一、选择题（每小题3分，共30分）

1．将二次函数y=x2+bx+c的图象先向左平移3个单位长度，再向上平移2个单位长度得到二次函数y=x2-2x+1的图象，则b,c的值分别是（ ）

2．已知a,b,c为非零的实数，且不全为正数，则a|a|+ab|ab|+ac|ac|+bc|bc|的所有可能结果的绝对值之和等于（ ）

3．分式方程2x-1-1=0的解是（ ）

4．如图，MN是半圆O的直径，K是MN延长线上一点，直线KP交半圆于点Q，P．若∠K=20°，∠PMQ=40°，则∠MQP等于（ ）

5．如图，点G、F分别是△BCD的边BC、CD上的点，BD的延长线与GF的延长线相交于点A，DE∥BC交GA于点E，则下列结论错误的是（ ）

6．下列图形中，对称轴条数最多的是（ ）

7．如图，平面直角坐标系中，点A，B的坐标分别为（-1，2），（-1，0），将△OAB绕点O顺时针旋转90°得到△OA1B1，点A1恰好落在反比例函数y=kx的图象上，则k的值是（ ）

8．如图，一架长2.5米的梯子AB斜靠在墙上，已知梯子底端B到墙角C的距离为1.5米，设梯子与地面所夹的锐角为α，则cosα的值为（ ）

9．在我国古代建筑中经常使用榫卯构件，如图是某种榫卯构件的示意图，其中卯的俯视图是（ ）

10．已知a,b为实数，且满足ab＞0，a+b-2=0，当a-b为整数时，ab的值为（ ）

二、填空题（每小题3分，共30分）

11．如图，邻边不等的矩形花圃ABCD，它的一边AD利用已有的围墙，另外三边所围的栅栏的总长度是6m.若矩形的面积为4m2，则AB的长度是m（可利用的围墙长度超过6m）．

12．计算232-54的结果是 ．

13．如图，长方形ABCD中，∠A=∠ABC=∠BCD=∠D=90°，AB=CD=3，AD=BC=5，点E为射线AD上的一个动点，△ABE与△FBE关于直线BE对称，当点E、F、C三点共线时，AE的长为 ．

14．把多项式2a2-4ab+2b2分解因式的结果是 ．

15．如图，AB为⊙O的直径，CD为⊙O的弦，∠ACD=25°40′，则∠BAD的度数为 ．

16．已知扇形的圆心角为120°，所对的弧长为8π3，则此扇形的面积是．

17．在函数y=3x2x+4中，自变量x的取值范围是 ．

18．如图，平面直角坐标系xOy中，点A（2，0），以OA为半径作⊙O，若点P，B都在⊙O上，且四边形AOPB为菱形，则点P的坐标为 ．

19．某市高新技术产业产值突破110亿元，数据“110亿”用科学记数法可表示为 ．

20．若实数a关于x的不等式组x3+1≥x+32x-1≥a+x2有解且最多3个整数解，则符合条件的a的取值范围是 ．

三、解答题：（21-22每题7分，23-24每题8分，25-27每题10分，共计60分）

22．电信部门要修建一座电视信号发射塔，如图所示，按照设计要求，发射塔到两个城镇A，B的距离相等，到两条高速公路OM和ON的距离也必须相等，发射塔应建在什么位置？在图上标出它的位置．

23．如图，AD是△ABC的中线，AE∥BC，BE交AD于点F，交AC于G，F是AD的中点．（1）求证：四边形ADCE是为平行四边形；（2）若EB是∠AEC的角平分线，请写出图中所有与AE相等的边．

24．先化简，再求值：aa-2÷（aa-2-4aa2-4），其中a=2+2．

1．将二次函数y=x²+bx+c的图象先向左平移3个单位长度，再向上平移2个单位长度得到二次函数y=x²-2x+1的图象，则b,c的值分别是（　　）

2．已知a,b,c为非零的实数，且不全为正数，则
a
|
a
|
+
ab
|
ab
|
+
ac
|
ac
|
+
bc
|
bc
|
的所有可能结果的绝对值之和等于（　　）

3．分式方程
2
x
-
1
-1=0的解是（　　）

4．如图，MN是半圆O的直径，K是MN延长线上一点，直线KP交半圆于点Q，P．若∠K=20°，∠PMQ=40°，则∠MQP等于（　　）

5．如图，点G、F分别是△BCD的边BC、CD上的点，BD的延长线与GF的延长线相交于点A，DE∥BC交GA于点E，则下列结论错误的是（　　）

6．下列图形中，对称轴条数最多的是（　　）

7．如图，平面直角坐标系中，点A，B的坐标分别为（-1，2），（-1，0），将△OAB绕点O顺时针旋转90°得到△OA₁B₁，点A₁恰好落在反比例函数y=
k
x
的图象上，则k的值是（　　）

8．如图，一架长2.5米的梯子AB斜靠在墙上，已知梯子底端B到墙角C的距离为1.5米，设梯子与地面所夹的锐角为α，则cosα的值为（　　）

9．在我国古代建筑中经常使用榫卯构件，如图是某种榫卯构件的示意图，其中卯的俯视图是（　　）

10．已知a,b为实数，且满足ab＞0，a+b-2=0，当a-b为整数时，ab的值为（　　）

11．如图，邻边不等的矩形花圃ABCD，它的一边AD利用已有的围墙，另外三边所围的栅栏的总长度是6m.若矩形的面积为4m²，则AB的长度是
m（可利用的围墙长度超过6m）．

12．计算2
3
2
-
54
的结果是

．

13．如图，长方形ABCD中，∠A=∠ABC=∠BCD=∠D=90°，AB=CD=3，AD=BC=5，点E为射线AD上的一个动点，△ABE与△FBE关于直线BE对称，当点E、F、C三点共线时，AE的长为
．

14．把多项式2a²-4ab+2b²分解因式的结果是

．

15．如图，AB为⊙O的直径，CD为⊙O的弦，∠ACD=25°40′，则∠BAD的度数为

．

16．已知扇形的圆心角为120°，所对的弧长为
8
π
3
，则此扇形的面积是
．

17．在函数y=
3
x
2
x
+
4
中，自变量x的取值范围是

．

18．如图，平面直角坐标系xOy中，点A（2，0），以OA为半径作⊙O，若点P，B都在⊙O上，且四边形AOPB为菱形，则点P的坐标为
．

19．某市高新技术产业产值突破110亿元，数据“110亿”用科学记数法可表示为
．

20．若实数a关于x的不等式组
x
3
+
1
≥
x
+
3
2
x
-
1
≥
a
+
x
2
有解且最多3个整数解，则符合条件的a的取值范围是
．

23．如图，AD是△ABC的中线，AE∥BC，BE交AD于点F，交AC于G，F是AD的中点．
（1）求证：四边形ADCE是为平行四边形；
（2）若EB是∠AEC的角平分线，请写出图中所有与AE相等的边．

24．先化简，再求值：
a
a
-
2
÷（
a
a
-
2
-
4
a
a
2
-
4
），其中a=
2
+2．