当前位置：试卷中心 > 试卷详情

2023年浙江省杭州市临平区中考数学二模试卷

发布：2025/11/26 10:0:10

一、选择题：本大题有10个小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．

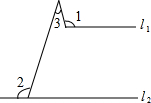1．如图，若l₁∥l₂，则∠1+∠2-∠3的度数为（　　）
A．180° B．360° C．90° D．60°
组卷：62引用：1难度：0.9
2．一副三角板按图1所示的位置摆放．将△DEF绕点A（F）逆时针旋转60°后（图2），测得CG=10cm,则两个三角形重叠（阴影）部分的面积为（　　）
A．75cm² B．（25+25
3
）cm²
C．（25+
25
3
3
）cm² D．（25+
50
3
3
）cm²
组卷：656引用：16难度：0.9
3．下列命题中属于真命题的是（　　）
A．两直线平行，内错角相等
B．同旁内角相等，两直线平行
C．若x²=9，则x=3
D．立方根等于其本身的数只有±1
组卷：85引用：3难度：0.8
4．我市某校开展“共创文明班，一起向未来”的古诗文朗诵比赛活动，有10位同学参加了初赛，按初赛成绩由高到低取前5位进入决赛．如果小王同学知道了自己的成绩后，要判断能否进入决赛，他需要知道这10位同学成绩的（　　）
A．平均数 B．众数 C．中位数 D．方差
组卷：1084引用：14难度：0.9
5．《九章算术》中有这样一个题：今有甲乙二人持钱不知其数．甲得乙半而钱五十，乙得甲太半而钱亦五十．问甲、乙持钱各几何？其意思为：今有甲乙二人，不知其钱包里有多少钱，若乙把其一半的钱给甲，则甲的钱数为50；而甲把其
2
3
的钱给乙，则乙的钱数也为50，问甲、乙各有多少钱？设甲的钱数为x,乙的钱数为y,则可建立方程组为（　　）
A．
x
+
1
2
y
=
50
2
3
x
+
y
=
50
B．
x
+
1
2
y
=
50
x
+
2
3
y
=
50
C．
1
2
x
+
y
=
50
2
3
x
+
y
=
50
D．
1
2
x
+
y
=
50
x
+
2
3
y
=
50
组卷：2523引用：44难度：0.6
6．已知a＞b,下列关系式中一定正确的是（　　）
A．a²＜b² B．2a＜2b C．a+2＜b+2 D．-a＜-b
组卷：2862引用：14难度：0.9
7．地球到月球的平均距离是384400000米，用科学记数法表示384400000是（　　）
A．3.844×10⁶ B．3.844×10⁸ C．38.44×10⁷ D．0.3844×10⁹
组卷：62引用：2难度：0.7
8．下列方程的变形中，正确的是（　　）
A．方程2x-1=x+5移项，得2x+x=5+1
B．方程
x
2
+
x
3
=1去分母，得3x+2x=1
C．方程-7x=4系数化为1，得x=-
7
4
D．方程（x+2）-2（x-1）=0去括号，得x+2-2x+2=0
组卷：273引用：3难度：0.9
9．计算-2²-（-2）³×（-1）²-（-1）³的结果为（　　）
A．5 B．-1 C．24 D．-30
组卷：300引用：3难度：0.7
10．在Rt△ABC中，∠ACB=90°，AC=2
3
，以点B为圆心，BC的长为半径作弧，交AB于点D，若点D为AB的中点，则阴影部分的面积是（　　）
A．2
3
-
2
3
π B．4
3
-
2
3
π C．2
3
-
4
3
π D．
2
3
π
组卷：2175引用：16难度：0.7

二、填空题：本题有6个小题，每小题4分，共24分．

11．某商品原价为a元，如果按原价的八折销售，那么售价是
元．（用含字母a的代数式表示）．
组卷：1480引用：17难度：0.5
12．一天，小青在校园内发现一棵树在阳光下的影子和她本人的影子在同一直线上，树顶的影子和她头顶的影子恰好落在地面的同一点，同时还发现她站立于树影的中点（如图所示）．如果小青的身高为1.5米，由此可推断出树高是

米．
组卷：119引用：2难度：0.7
13．不等式组
5
-
x
≤
1
x
-
3
2
＜
2
的解集为
．
组卷：167引用：4难度：0.8
14．分解因式：4x³-4x=

．
组卷：176引用：8难度：0.7
15．如图，已知点C（0，1），直线y=x+6与两坐标轴分别交于A，B两点．点D，E分别是OB，AB上的动点，则△CDE周长的最小值是
．
组卷：593引用：1难度：0.6
16．如图，半圆O的直径AB=7，两弦AC、BD相交于点E，弦CD=
7
2
，且BD=5，则DE=
．
组卷：481引用：7难度：0.7

三、解答题：本题有7个小题，共66分．解答应写出文字说明、证明过程或演算步骤．

17．已知：如图，点E、F在BC上，AF与DE交于点G，AB=DC，GE=GF，∠B=∠C．求证：AG=DG．
组卷：1619引用：5难度：0.8
18．如图，在菱形ABCD中，∠ABC=120°，AB=4
3
，E为对角线AC上的动点（点E不与A，C重合），连接BE，将射线EB绕点E逆时针旋转120°后交射线AD于点F．
（1）如图1，当AE=AF时，求∠AEB的度数；
（2）如图2，分别过点B，F作EF，BE的平行线，且两直线相交于点G．
i）试探究四边形BGFE的形状，并求出四边形BGFE的周长的最小值；
ii）连接AG，设CE=x,AG=y,请直接写出y与x之间满足的关系式，不必写出求解过程．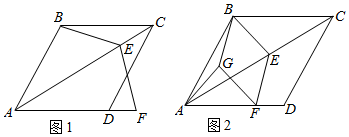
组卷：1187引用：3难度：0.1
19．如图所示，△ABC内接于⊙O，AB为⊙O直径，BE交AC延长线于点E，D为
ˆ
AC
上一点，连接BD，DC，已知∠BDC=∠CBE．
（1）求证：BE为⊙O切线；
（2）若
tan
∠
BAC
=
4
3
，BC=2，求BE的长．
组卷：62引用：1难度：0.6
20．如图，反比例函数y₁=
k
x
与一次函数y₂=-x+b的图象交于两点A（1，3）、B（3，1）．
（1）反比例函数和一次函数的解析式；
（2）观察图象，请直接写出满足y₁≤y₂的取值范围；
（3）若x轴上的存在一点Q，使△QAB的周长最小，请直接写出点Q的坐标．
组卷：228引用：2难度：0.6
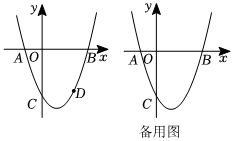21．已知抛物线y=x²-（2m-1）x-2m的最低点的纵坐标为-4，它与x轴交于点A和B（点A在原点左侧点B在原点右侧），与y轴交于点C．
（1）求抛物线的解析式；
（2）如图1，点D是抛物线的一点，与点C关于抛物线对称轴对称，点
P
（
1
2
nkn
+
1
）
，n为任意实数，当n变化时，点P在直线l上运动，若点A，D到直线l的距离相等，求k的值；
（3）将该抛物线在0≤x≤4间的部分记为图象G，将图象G在直线y=t下方的部分沿y=t翻折，其余部分保持不变，得到一个新的函数的图象，记这个函数的最大值为m,最小值为n,若m-n≤7．求t的取值范围．
组卷：348引用：2难度：0.2
22．根据频数分布表或频数分布直方图求加权平均数时，统计中常用各组的组中值代表各组的实际数据，把各组的频数看作相应组中值的权，请你依据以上知识，解决下面的实际问题．
为了解5路公共汽车的运营情况，公交部门统计了某天5路公共汽车每个运行班次的载客量，并按载客量的多少分成A，B，C，D四组，得到如下统计图：

（1）求A组对应扇形圆心角的度数，并写出这天载客量的中位数所在的组；
（2）求这天5路公共汽车平均每班的载客量；
（3）如果一个月按30天计算，请估计5路公共汽车一个月的总载客量，并把结果用科学记数法表示出来．
组卷：536引用：4难度：0.3
23．解方程：
（1）4-x=3（1+x）
（2）x-
x
-
1
2
=
2
-
x
+
2
3
．
组卷：24引用：1难度：0.5