当前位置：试卷中心 > 试卷详情

2020年湖北省十堰市竹溪县中考数学一诊试卷

发布：2025/11/26 10:0:10

一、选择题（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的.

1．对于任意有理数a,b,定义运算“※”如下：a※b=（a-b）²+ab,则当（m-1）※（m+1）=12时，m的值为（　　）
A．3 B．4 C．±3 D．±4
组卷：69引用：1难度：0.6
2．正比例函数y=x与反比例函数y=
1
x
的图象相交于A，C两点，AB⊥x轴于点B，CD⊥x轴于点D（如图），则四边形ABCD的面积为（　　）
A．1 B．2 C．4 D．8
组卷：1719引用：15难度：0.7
3．
3
4
的相反数是（　　）
A．
4
3
B．
-
4
3
C．
3
4
D．
-
3
4
组卷：169引用：45难度：0.9
4．如图是两户居民家庭全年各项支出的统计图，根据统计图，下列对两户教育支出占全年总支出的百分比作出的判断中，正确的是（　　）
A．甲户比乙户大 B．乙户比甲户大
C．甲，乙两户一样大 D．无法确定哪一户大
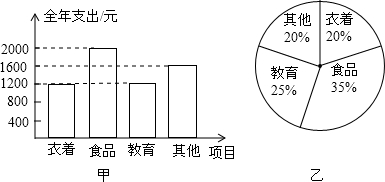组卷：942引用：52难度：0.5
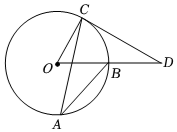5．如图，AB、AC是⊙O的两条弦，∠BAC=25°，过点C的切线与OB的延长线交于点D，则∠D的度数为（　　）
A．25° B．30° C．35° D．40°
组卷：1632引用：75难度：0.7
6．墨斗被认为是“百作手艺祖师爷”鲁班的发明，是木匠用来弹、放各种线记的重要工具，以其“绳之以墨”的功能成为了文人墨客心中正直的化身．如图，经过刨平的木板上的两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是（　　）
A．垂线段最短 B．线段有两个端点
C．两点之间线段最短 D．两点确定一条直线
组卷：144引用：4难度：0.8
7．如图，各正方形中的四个数之间都有相同的规律，根据此规律，x的值为（　　）
A．242 B．232 C．220 D．252
组卷：457引用：6难度：0.7
8．2022年北京冬奥会以及冬残奥会的吉祥物冰墩墩和雪容融，受到了国内外网友的热烈欢迎，某加工厂接到紧急加工冰墩墩的任务，原计划每天完成1200只，实际每天比原计划多加工600只，结果提前3天完成任务，设原计划x天完成任务，则可列方程为（　　）
A．1200x=（1200+600）（x-3）
B．1200（x-3）=（1200+600）x
C．1200x=（1200-600）（x+3）
D．1200（x+3）=（1200-600）x
组卷：48引用：2难度：0.8
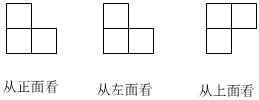9．由4个相同的小正方体搭建了一个积木，从不同方向看积木，所得到的图形如图所示，则这个积木可能是（　　）
A． B． C． D．
组卷：127引用：4难度：0.7
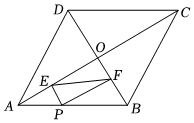10．如图，菱形ABCD的对角线AC，BD相交于点O，点P为AB边上一动点（不与点A，B重合），PE⊥OA于点E，PF⊥OB于点F．若AC=20，BD=10，则EF的最小值为（　　）
A．
2
2
B．
2
3
C．4 D．
2
5
组卷：1771引用：9难度：0.5

二、填空题（本题有6个小题，每小题3分，共18分）

11．分解因式：a²-ab=
．
组卷：4210引用：86难度：0.7
12．如图，等腰△ABC的底边BC=20，面积为160，点F是BC边上的一个动点，EG是腰AC的垂直平分线，若点D在EG上运动，则CD+DF的最小值为
．
组卷：401引用：6难度：0.7
13．如图，两个形状为正十边形的纪念币一边重合放置在一起，则∠α=
度．
组卷：150引用：3难度：0.9
14．不等式-4x≥-12的正整数解为

．
组卷：970引用：45难度：0.7
15．在半径为6cm的圆中，50°的圆心角所对的弧长为
cm.
组卷：183引用：4难度：0.6
16．小明将2004年雅典奥运会中国男子篮球队队员的年龄情况绘制成了如图所示的条形统计图，则中国篮球队共有
名队员．
组卷：48引用：17难度：0.7

三、解答题（本题有9个小题，共72分）

17．已知，足球球门高2.44米，宽7.32米（如图1）在射门训练中，一球员接传球后射门，击球点A距离地面0.4米，即AB=0.4米，球的运动路线是抛物线的一部分，当球的水平移动距离BC为6米时，球恰好到达最高点D，即CD=4.4米．以直线BC为x轴，以直线AB为y轴建立平面直角坐标系（如图2）．

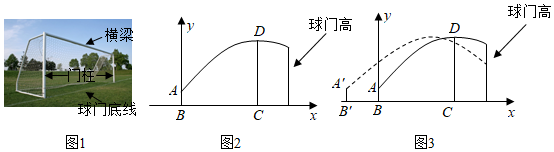
（1）求该抛物线的表达式；
（2）若足球恰好击中球门横梁，求该足球运动的水平距离；
（3）若要使球直接落在球门内，则该球员应后退m米后接球射门，击球点为A'（如图3），请直接写出m的取值范围．
组卷：1120引用：7难度：0.2

18．疫情防控，人人有责．为了增强未成年学生的疫情防控意识，某中学举行了一次疫情防控知识竞赛活动（竞赛成绩为百分制）．数学兴趣小组随机抽取了部分学生的竞赛成绩进行了统计分析，制作了如下不完整的频数分布表．请根据表中信息完成下列问题：
（1）数学兴趣小组共抽取了
名学生的竞赛成绩进行了统计分析，频数分布表中a=
，b=
；

竞赛成绩分组频数频率

A组（60≤x＜70） a 0.20

B组（70≤x＜80） 14 0.28

C组（80≤x＜90） 22 b

D组（90≤x≤100） 4 0.08

（2）若该校共有1500名学生参加了这次知识竞赛活动，估计该校参赛成绩不低于80分的有
人；
（3）学校要从D组甲、乙、丙、丁四名学生中任选两人担任“疫情防控宣传员”，请用画树状图或列表法求恰好选到甲和乙的概率．

组卷：43引用：1难度：0.7

19．计算：（
1
2
）^-1+（π-1）⁰-2cos30°+|
3
-1|
组卷：20引用：1难度：0.7
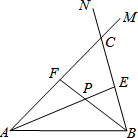20．在线段AB的同侧作射线AM和BN，若∠MAB与∠NBA的平分线分别交射线BN，AM于点E，F，AE和BF交于点P．如图，点点同学发现当射线AM，BN交于点C；且∠ACB=60°时，有以下两个结论：
①∠APB=120°；②AF+BE=AB．
那么，当AM∥BN时：
（1）点点发现的结论还成立吗？若成立，请给予证明；若不成立，请求出∠APB的度数，写出AF，BE，AB长度之间的等量关系，并给予证明；
（2）设点Q为线段AE上一点，QB=5，若AF+BE=16，四边形ABEF的面积为32
3
，求AQ的长．
组卷：2349引用：4难度：0.1
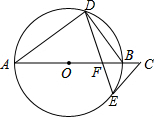21．如图，AB是⊙O的直径，点D、E在⊙O上，∠A=2∠BDE，点C在AB的延长线上，∠C=∠ABD．
（1）求证：CE是⊙O的切线；
（2）连接BE，求证：∠CEB=∠BDE；
（3）若BF=2，EF=
11
，求⊙O的半径长．
组卷：120引用：1难度：0.7
22．先化简，再求值：（
3
x
x
-
2
-
x
x
+
2
）÷
x
x
2
-
4
，在-2，0，1，2四个数中选一个合适的代入求值．
组卷：2431引用：61难度：0.7
23．已知关于x的方程x²-2x+k-1=0，设方程的两个根是x₁，x₂，若2x₁x₂＞x₁+x₂-3成立，求k的取值范围．
组卷：66引用：1难度：0.5
24．如图，小东在教学楼距地面9m高的窗口C处，测得正前方旗杆顶部A点的仰角为37°，旗杆底部B点的俯角为45°．
（1）求旗杆AB的高．（结果精确到0.01m,参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）
（2）升旗时，国旗上端悬挂在距地面2.25m处．若国旗随国歌声冉冉升起，并在国歌播放45秒结束时到达旗杆顶端，则国旗应以每秒多少米的速度匀速上升？
组卷：132引用：3难度：0.5
25．已知如图1，在以O为原点的平面直角坐标系中，抛物线y=
1
4
x²+bx+c与x轴交于A，B两点，与y轴交于点C（0，-1），连接AC，AO=2CO，直线l过点G（0，t）且平行于x轴，t＜-1．
（1）求抛物线对应的二次函数的解析式；
（2）①若D（-4，m）为抛物线y=
1
4
x²+bx+c上一定点，点D到直线l的距离记为d,当d=DO时，求t的值；
②若为抛物线y=
1
4
x²+bx+c上一动点，点D到①中的直线l的距离与OD的长是否恒相等，说明理由；
（3）如图2，若E，F为上述抛物线上的两个动点，且EF=8，线段EF的中点为M，求点M纵坐标的最小值．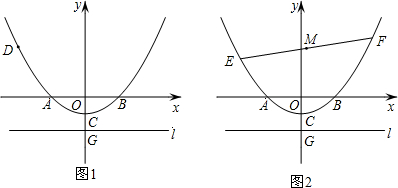
组卷：147引用：1难度：0.5