当前位置：试卷中心 > 试卷详情

2022年福建省厦门市湖里区中考数学二模试卷

发布：2025/11/26 10:0:8

一、选择题：本大题有10小题，每小题4分，共40分.每小题都有四个选项，其中有且只有一个选项正确.

1．一个几何体的边面全部展开后铺在平面上，不可能是（　　）
A．一个三角形 B．一个圆
C．三个正方形 D．一个小圆和半个大圆
组卷：109引用：4难度：0.7
2．以下结论中（　　）个结论不正确．
（1）1既不是合数也不是质数；
（2）大于0的偶数中只有一个数不是合数；
（3）个位数字是5的自然数中，只有一个数不是合数；
（4）各位数字之和是3的倍数的自然数，个个都是合数．
A．1 B．2 C．3 D．4
组卷：141引用：3难度：0.9
3．已知a、b、c均为有理数，则a+b-c的相反数是（　　）
A．b+a-c B．-b-a-c C．-b-a+c D．b-a+c
组卷：48引用：1难度：0.9
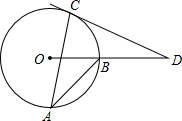4．如图，AB、AC是⊙O的两条弦，∠A=25°，过点C的切线与OB的延长线交于点D，则∠D的度数（　　）
A．25° B．30° C．40° D．50°
组卷：334引用：8难度：0.7
5．在△ABC中，∠C=90°，∠B=α，BC=m,那么边AC的长为（　　）
A．msinα B．mcosa C．mtanα D．mcotα
组卷：17引用：3难度：0.5
6．下列计算正确的是（　　）
A．（2a）³÷a=8a² B．
（
-
2
ab
）
（
-
1
2
a
2
）
=
a
2
b
C．（a-b）²=a²-b² D．
-
4
（
1
4
a
-
1
）
=
-
a
-
4
组卷：157引用：44难度：0.9

7．下列说法正确的是（　　）

A．某市“明天降雨的概率是75%”表示明天有75%的时间会降雨

B．随机抛掷一枚均匀的硬币，落地后正面一定朝上

C．在一次抽奖活动中，“中奖的概率是

100

”表示抽奖100次就一定会中奖

D．在平面内，平行四边形的两条对角线一定相交

组卷：210引用：38难度：0.9

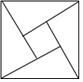8．“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲．如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为a,较短直角边长为b.若ab=8，大正方形的面积为25，则小正方形的边长为（　　）
A．9 B．6 C．4 D．3
组卷：8406引用：68难度：0.7
9．甲、乙两公司全体员工踊跃参与“携手防疫，共渡难关”捐款活动，甲公司共捐款80000元，乙公司共捐款160000元，甲公司的人数比乙公司少40人，乙公司的人均捐款数是甲公司的
10
7
，求甲、乙两公司各有多少人？设甲公司有x人，则乙公司有（x+40）人，根据题意，下列方程中符合题意的是（　　）
A．
80000
x
×
10
7
=
160000
x
+
40
B．
80000
x
=
160000
x
+
40
×
10
7
C．
80000
x
×
7
10
=
160000
x
+
40
D．
80000
x
=
160000
x
+
40
×
7
10
组卷：38引用：2难度：0.8
10．若二次函数y=ax²+bx+c（a≠0）的图象与x轴有两个交点，坐标分别为（x₁，0），（x₂，0），且x₁＜x₂，图象上有一点M（x₀，y₀）在x轴下方，则下列判断正确的是（　　）
A．a＞0 B．b²-4ac≥0
C．x₁＜x₀＜x₂ D．a（x₀-x₁）（x₀-x₂）＜0
组卷：2247引用：85难度：0.7

二、填空题：本题共6小题，每小题4分，共24分.

11．计算：（-9）-（-6）=

；24-（-32）=

．
组卷：60引用：1难度：0.9
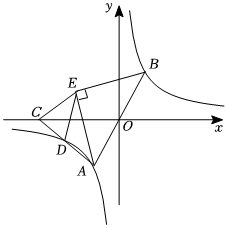12．如图，过原点的直线与反比例函数y=
k
x
（k＞0）交于A、B两点，点A在第三象限，点C在x轴的负半轴上，连接AC交反比例函数于点D，AE为∠CAB的角平分线，过点B作BE⊥AE，连DE，若D为AC中点，△ADE面积为12，则k的值为
．
组卷：186引用：1难度：0.4
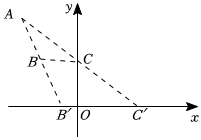13．如图，平面直角坐标系中，一点光源位于A（-3，4），线段BC的两个端点坐标分别为B（-2，2）与C（0，2），则线段BC在x轴上的影子B′C′的长度为
．
组卷：707引用：3难度：0.8
14．一元一次不等式3x-2＜0的解集为

．
组卷：82引用：3难度：0.5
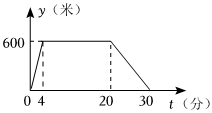15．亮亮从家跑步到学校，在学校图书馆看了一会书，然后步行回家，亮亮离家的路程y（米）与时间t（分）之间的关系如图所示，则亮亮回家的速度为
．
组卷：449引用：3难度：0.7
16．中国航母辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰，满载排水量为67500吨，这个数据用科学记数法可表示为
．
组卷：303引用：73难度：0.7

三、解答题：本题共9小题，共86分.

17．如图1，P为Rt△ABC所在平面内任意一点（不在直线AC上），∠ACB=90°，M为AB边中点．操作：以PA、PC为邻边作平行四边形PADC，连续PM并延长到点E，使ME=PM，连接DE．
探究：
（1）请猜想与线段DE有关的三个结论；
（2）请你利用图2，图3选择不同位置的点P按上述方法操作；
（3）经历（2）之后，如果你认为你写的结论是正确的，请加以证明；
如果你认为你写的结论是错误的，请用图2或图3加以说明；
（注意：错误的结论，只要你用反例给予说明也得分）
（4）若将“Rt△ABC”改为“任意△ABC”，其他条件不变，利用图4操作，并写出与线段DE有关的结论（直接写答案）．
组卷：4033引用：28难度：0.1
18．已知y+3与x成正比例，且x=2时，y=7．
（1）求y关于x的函数解析式；
（2）当x=-1时，求y的值．
组卷：214引用：2难度：0.7
19．化简求值，（
2
x
+
7
x
+
3
+
x
-
1
）÷
x
2
+
2
x
x
+
3
，其中x是不等式组
x
+
3
＜
0
2
x
+
9
＞
0
的整数解．
组卷：504引用：3难度：0.6
20．某超市的地面需要铺设地砖，经询问得知：若请甲、乙两个工程队同时施工，8天可以完成，需付两工程队费用共8000元．若先请甲工程队单独做6天，再请乙工程队单独做，则乙工程队12天可以完成，需付两工程队费用共7920元，问：
（1）甲、乙两工程队单独工作一天，超市应各付多少元？
（2）单独请哪个工程队，超市所付费用较少？
组卷：55引用：1难度：0.6
21．已知x=
1
2
+
3
，y=
1
2
-
3
．
（1）求代数式2x²+2y²-xy的值；
（2）求代数式
x
2
-
x
3
x
2
-
6
x
+
3
-xy的值．
组卷：938引用：4难度：0.8
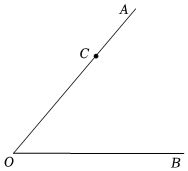22．如图，点C在∠AOB的边OA上，选择合适的工具按要求画图．
（1）反向延长射线OB，得到射线OD；
（2）在射线OD上取一点F，使得OF=OC；
（3）在∠AOD内部画射线OE；
（4）在射线OE上取一点P，使得CP+FP最小；
（5）对于（4）中的结论，依据是
．
组卷：30引用：3难度：0.5
23．已知：如图，▱ABCD中，AD=3cm,CD=1cm,∠B=45°，点P从点A出发，沿AD方向匀速运动，速度为3cm/s；点Q从点C出发，沿CD方向匀速运动，速度为1cm/s,连接并延长QP交BA的延长线于点M，过M作MN⊥BC，垂足是N，设运动时间为t（s）（0＜t＜1）
解答下列问题：
（1）当t为何值时，四边形AQDM是平行四边形？
（2）设四边形ANPM的面积为y（cm²），求y与t之间的函数关系式：
（3）是否存在某一时刻t,使四边形ANPM的面积是平行四边形ABCD的面积的一半？若存在，求出相应的t值；若不存在，说明理由．
（4）连接AC，是否存在某一时刻t,使NP与AC的交点把线段AC分成
2
：1的两部分？若存在，求出相应的t值；若不存在，说明理由．
组卷：1252引用：7难度：0.5
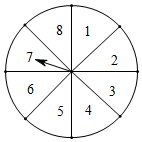24．今年“五一”假期期间，某超市开展有奖促销活动，凡在超市购物的顾客均有转动圆盘的机会（如图），如果规定当圆盘停下来时指针指向8就中一等奖，指向2或6就中二等奖，指向1或3或5就中三等奖；指向其余数字不中奖．
（1）转动转盘中一等奖、二等奖、三等奖的概率是分别是多少？
（2）顾客中奖的概率是多少？
（3）“五一”这天有1800人参与这项活动，估计获得一等奖的人数是多少？
组卷：1081引用：6难度：0.7
25．如图，抛物线y=-x²+bx+c与一次函数y=x+1的图象相交于点A、B，点B的纵坐标为3，点P是抛物线上的动点．
（1）求b、c的值；
（2）若点P在直线AB上方，设点P的横坐标为n,△PAB的面积为S，求S关于n的函数关系式；
（3）设点P关于直线AB的对称点为M，直接写出当四边形PAMB为菱形时点P的横坐标．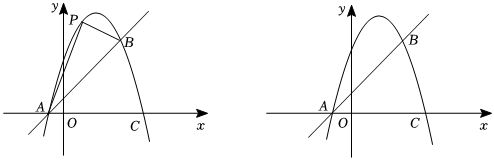
组卷：17引用：1难度：0.3

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．一个三角形	B．一个圆
C．三个正方形	D．一个小圆和半个大圆

A．（2a）³÷a=8a²	B．（ - 2 ab ）（ - 1 2 a 2 ） = a 2 b
C．（a-b）²=a²-b²	D． - 4 （ 1 4 a - 1 ） = - a - 4

A．a＞0	B．b²-4ac≥0
C．x₁＜x₀＜x₂	D．a（x₀-x₁）（x₀-x₂）＜0

2022年福建省厦门市湖里区中考数学二模试卷

一、选择题：本大题有10小题，每小题4分，共40分.每小题都有四个选项，其中有且只有一个选项正确.

1．一个几何体的边面全部展开后铺在平面上，不可能是（ ）

2．以下结论中（ ）个结论不正确．（1）1既不是合数也不是质数；（2）大于0的偶数中只有一个数不是合数；（3）个位数字是5的自然数中，只有一个数不是合数；（4）各位数字之和是3的倍数的自然数，个个都是合数．

3．已知a、b、c均为有理数，则a+b-c的相反数是（ ）

4．如图，AB、AC是⊙O的两条弦，∠A=25°，过点C的切线与OB的延长线交于点D，则∠D的度数（ ）

5．在△ABC中，∠C=90°，∠B=α，BC=m,那么边AC的长为（ ）

6．下列计算正确的是（ ）

7．下列说法正确的是（ ）

10．若二次函数y=ax2+bx+c（a≠0）的图象与x轴有两个交点，坐标分别为（x1，0），（x2，0），且x1＜x2，图象上有一点M（x0，y0）在x轴下方，则下列判断正确的是（ ）

二、填空题：本题共6小题，每小题4分，共24分.

11．计算：（-9）-（-6）= ；24-（-32）= ．

12．如图，过原点的直线与反比例函数y=kx（k＞0）交于A、B两点，点A在第三象限，点C在x轴的负半轴上，连接AC交反比例函数于点D，AE为∠CAB的角平分线，过点B作BE⊥AE，连DE，若D为AC中点，△ADE面积为12，则k的值为 ．

13．如图，平面直角坐标系中，一点光源位于A（-3，4），线段BC的两个端点坐标分别为B（-2，2）与C（0，2），则线段BC在x轴上的影子B′C′的长度为 ．

14．一元一次不等式3x-2＜0的解集为 ．

15．亮亮从家跑步到学校，在学校图书馆看了一会书，然后步行回家，亮亮离家的路程y（米）与时间t（分）之间的关系如图所示，则亮亮回家的速度为 ．

16．中国航母辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰，满载排水量为67500吨，这个数据用科学记数法可表示为 ．

三、解答题：本题共9小题，共86分.

18．已知y+3与x成正比例，且x=2时，y=7．（1）求y关于x的函数解析式；（2）当x=-1时，求y的值．

19．化简求值，（2x+7x+3+x-1）÷x2+2xx+3，其中x是不等式组x+3＜02x+9＞0的整数解．

21．已知x=12+3，y=12-3．（1）求代数式2x2+2y2-xy的值；（2）求代数式x2-x3x2-6x+3-xy的值．

1．一个几何体的边面全部展开后铺在平面上，不可能是（　　）

2．以下结论中（　　）个结论不正确．
（1）1既不是合数也不是质数；
（2）大于0的偶数中只有一个数不是合数；
（3）个位数字是5的自然数中，只有一个数不是合数；
（4）各位数字之和是3的倍数的自然数，个个都是合数．

3．已知a、b、c均为有理数，则a+b-c的相反数是（　　）

4．如图，AB、AC是⊙O的两条弦，∠A=25°，过点C的切线与OB的延长线交于点D，则∠D的度数（　　）

5．在△ABC中，∠C=90°，∠B=α，BC=m,那么边AC的长为（　　）

6．下列计算正确的是（　　）

7．下列说法正确的是（　　）

10．若二次函数y=ax²+bx+c（a≠0）的图象与x轴有两个交点，坐标分别为（x₁，0），（x₂，0），且x₁＜x₂，图象上有一点M（x₀，y₀）在x轴下方，则下列判断正确的是（　　）

11．计算：（-9）-（-6）=

；24-（-32）=

．

12．如图，过原点的直线与反比例函数y=
k
x
（k＞0）交于A、B两点，点A在第三象限，点C在x轴的负半轴上，连接AC交反比例函数于点D，AE为∠CAB的角平分线，过点B作BE⊥AE，连DE，若D为AC中点，△ADE面积为12，则k的值为
．

13．如图，平面直角坐标系中，一点光源位于A（-3，4），线段BC的两个端点坐标分别为B（-2，2）与C（0，2），则线段BC在x轴上的影子B′C′的长度为
．

14．一元一次不等式3x-2＜0的解集为

．

15．亮亮从家跑步到学校，在学校图书馆看了一会书，然后步行回家，亮亮离家的路程y（米）与时间t（分）之间的关系如图所示，则亮亮回家的速度为
．

16．中国航母辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰，满载排水量为67500吨，这个数据用科学记数法可表示为
．

18．已知y+3与x成正比例，且x=2时，y=7．
（1）求y关于x的函数解析式；
（2）当x=-1时，求y的值．

19．化简求值，（
2
x
+
7
x
+
3
+
x
-
1
）÷
x
2
+
2
x
x
+
3
，其中x是不等式组
x
+
3
＜
0
2
x
+
9
＞
0
的整数解．

21．已知x=
1
2
+
3
，y=
1
2
-
3
．
（1）求代数式2x²+2y²-xy的值；
（2）求代数式
x
2
-
x
3
x
2
-
6
x
+
3
-xy的值．