2023年北师大新版九年级（上）《1.3 正方形的性质与判定》新题套卷（1）

一、选择题（共10小题）

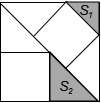• 1．有3个正方形如图所示放置，阴影部分的面积依次记为S₁，S₂，则S₁：S₂等于（　　）

  A．1： 2

  B．1：2

  C．2：3

  D．4：9
  组卷：4359引用：16难度：0.7

  解析

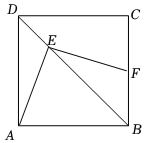• 2．如图，点E是正方形ABCD对角线BD上一点，连接AE，过点E作EF⊥AE，交BC于点F．已知DE=

  2

  ，则CF的长为（　　）

  A． 2

  B．2

  C． 6

  D．2 2
  组卷：800引用：7难度：0.6

  解析

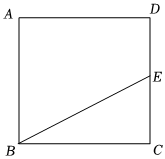• 3．如图，正方形ABCD的边长为8，点E在CD边上，CE=4，若点F在正方形的某一边上，满足CF=BE，且CF与BE的交点为M，则CM的长度为（　　）

  A．2或 8 5 5

  B． 2 5 或 8 5 5

  C． 4 5 5 或 8 5 5

  D． 4 5 5 或 2 5
  组卷：232引用：2难度：0.5

  解析

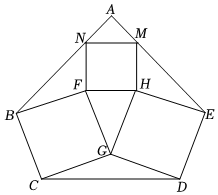• 4．如图所示，正方形BCGF，HGDE，FHMN内接于五边形ABCDE，该五边形是轴对称图形，AB与AE为对称边，∠A=90°，AN=AM，则

  CD

  AN

  的值是（　　）

  A． 3 2

  B． 3 2 2

  C． 2

  D． 2 2
  组卷：88引用：1难度：0.5

  解析

• 5．如图，点P的坐标为（2，2），点A，B分别在x轴，y轴的正半轴上运动，且∠APB=90°，下列结论：
  ①PA=PB；
  ②当OA=OB时四边形OAPB是正方形；
  ③四边形OAPB的面积和周长都是定值；
  ④连接OP，AB，则AB＞OP，其中正确的有（　　）

  A．①②

  B．①②③

  C．①②④

  D．①②③④
  组卷：463引用：5难度：0.4

  解析

• 6．下列说法错误的是（　　）

  A．对角线互相垂直的四边形是菱形

  B．对角线相等的平行四边形是矩形

  C．对角线相等且垂直的平行四边形是正方形

  D．一组对边平行且相等的四边形是平行四边形
  组卷：179引用：6难度：0.7

  解析

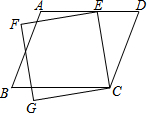• 7．如图，有一个平行四边形ABCD和一个正方形CEFG，其中点E在边AD上．若∠ECD=40°，∠AEF=15°，则∠B的度数为（　　）

  A．55°

  B．60°

  C．65°

  D．75°
  组卷：24引用：1难度：0.6

  解析

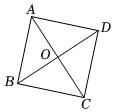• 8．如图3，要使▱ABCD是正方形，需增加条件．在条件①AB=BC，②AC=BD，③AC⊥BD，④∠ABC=90°中选取两个作为条件，不正确的是（　　）

  A．①和②

  B．①和③

  C．②和③

  D．③和④
  组卷：47引用：1难度：0.6

  解析

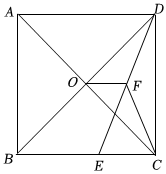• 9．如图，正方形ABCD的对角线AC与BD相交于点O，E为BC上的一点，CE=5，F为DE的中点．若△CEF的周长为18，则OF的长为（　　）

  A．4.5

  B．4

  C．3

  D．3.5
  组卷：137引用：3难度：0.5

  解析

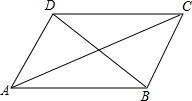• 10．如图，小明在学习了正方形之后，给同桌小文出了道题，从下列四个条件：①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD中任选两个作为补充条件，使▱ABCD为正方形．现有下列四种选法，你认为其中错误的是（　　）

  A．②③

  B．①③

  C．①②

  D．③④
  组卷：1695引用：12难度：0.5

  解析

二、填空题（共5小题）

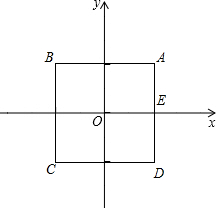• 11．如图，正方形ABCD的各边分别平行于x轴或者y轴，蚂蚁甲和蚂蚁乙都由点（3，0）出发，同时沿正方形ABCD的边做环绕运动，蚂蚁甲按顺时针方向以3个单位长度/秒的速度做匀速运动，蚂蚁乙按逆时针方向以1个单位长度/秒的速度做匀速运动，则两只蚂蚁出发后第三次相遇点的坐标是

  ．
  组卷：270引用：5难度：0.5

  解析

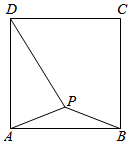• 12．如图，点P是正方形ABCD内一点，连接AP、BP、DP，若AP=1，PD=

  10

  ，∠APB=135°，则正方形ABCD的面积为

  ．
  组卷：375引用：2难度：0.6

  解析

• 13．正方形判定：有一组邻边相等的

  是正方形．
  组卷：26引用：1难度：0.9

  解析

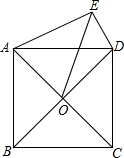• 14．如图，正方形ABCD的对角线交于点O，以AD为边向外作Rt△ADE，∠AED=90°，连接OE，DE=6，OE=8

  2

  ，则另一直角边AE的长为

  ．
  组卷：2987引用：6难度：0.5

  解析

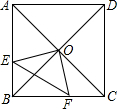• 15．在正方形ABCD中，O是对角线AC、BD的交点，过O作OE⊥OF，分别交AB、BC于E、F，若AE=4，CF=3，则EF的长为

  ．
  组卷：590引用：10难度：0.7

  解析

三、解答题（共5小题）

• 16．在正方形ABCD中，点P是CD边上一动点，连接PA，分别过点B、D作BE⊥PA、DF⊥PA，垂足分别为E、F，如图①．
  （1）请探究BE、DF、EF这三条线段的长度具有怎样的数量关系？若点P在DC的延长线上，如图②，那么这三条线段的长度之间又具有怎样的数量关系？若点P在CD的延长线上呢，如图③，请分别直接写出结论；
  （2）就（1）中的三个结论选择一个加以证明．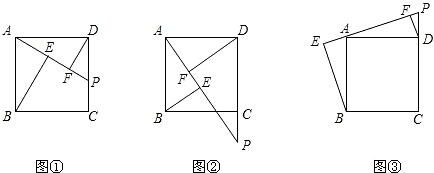
  
  组卷：1027引用：38难度：0.1

  解析

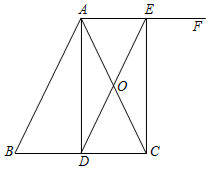• 17．如图，AD是等腰△ABC底边BC上的高，AF∥BC，点O是AC中点，连结DO并延长交AF于点E，连结CE．
  （1）求证：四边形ADCE是矩形；
  （2）①若AB=17，BC=16，则四边形ADCE的面积是多少；
  ②当∠BAC为多少度时，四边形ADCE是正方形．
  组卷：305引用：1难度：0.5

  解析

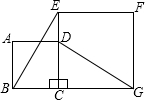• 18．如图，正方形ABCD的边CD在正方形ECGF的边CE上，连接BE、DG．
  （1）观察猜想BE与DG之间的大小关系，并证明你的结论；
  （2）图中是否存在通过旋转能够互相重合的两个三角形？若存在，请说出旋转过程；若不存在，请说明理由．
  组卷：741引用：93难度：0.3

  解析

• 19．如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且FD=BE，连接CE，CF．求证：CE=CF．
  组卷：160引用：5难度：0.7

  解析

• 20．如图，在平行四边形ABCD中，∠BAC=90°，AB=AC，过点A作边BC的垂线AF交DC的延长线于点E，点F是垂足，连接BE、DF，DF交AC于点O．求证：
  （1）四边形ABEC是正方形；
  （2）

  DE

  =

  2

  BC

  ；
  （3）S_△CFD=S_△BEF．
  组卷：180引用：2难度：0.6

  解析