2023-2024学年北京市朝阳区蒋府实验学校八年级（上）期中数学试卷

一、选择题（共24分，每题3分）第1-8题均有四个选项，符合题意的选项只有一个.

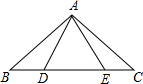• 1．如图，已知△ABE≌△ACD，AB=AC，BE=CD，∠B=40°，∠AEC=120°，则∠DAC的度数为（　　）

  A．80°

  B．70°

  C．60°

  D．50°
  组卷：53引用：2难度：0.9

  解析

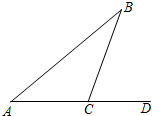• 2．如图是一失事飞机的残骸图形，若∠B=30°，∠BCD=70°，那么∠A的度数是（　　）

  A．30°

  B．40°

  C．60°

  D．70°
  组卷：160引用：3难度：0.9

  解析

• 3．下列体育运动项目图标中，是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：136引用：5难度：0.8

  解析

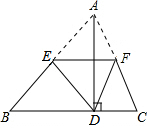• 4．如图，在△ABC中，AB=10，AC=8，BC=12，AD⊥BC于D，点E、F分别在AB、AC边上，把△ABC沿EF折叠，使点A与点D恰好重合，则△DEF的周长是（　　）

  A．14

  B．15

  C．16

  D．17
  组卷：813引用：43难度：0.9

  解析

• 5．下列说法中错误的是（　　）

  A．三角形的三条角平分线相交于三角形内一点

  B．三角形的三条中线相交于三角形内一点

  C．三角形的三条高所在的直线相交于三角形内一点

  D．等边三角形三边的垂直平分线相交于三角形内一点
  组卷：291引用：2难度：0.9

  解析

• 6．已知三角形两条边的长分别是3和4，则第三边长可能是（　　）

  A．1

  B．5

  C．7

  D．9
  组卷：2引用：2难度：0.6

  解析

• 7．若等腰三角形的一边长为10，另一边长为7，则它的周长为（　　）

  A．17

  B．24

  C．27

  D．24或27
  组卷：87引用：8难度：0.9

  解析

• 8．已知一个n边形的每个外角都等于60°，则n的值是（　　）

  A．5

  B．6

  C．7

  D．8
  组卷：684引用：7难度：0.8

  解析

二、填空题（共24分，每题3分）

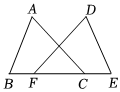
• 9．如图，△ABC≌△DEF，若BC=4，则EF的长为

  ．
  ​
  组卷：13引用：1难度：0.7

  解析

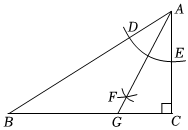• 10．如图，在△ABC中，∠C=90°，以点A为圆心，以任意长为半径作弧，分别交AB，AC于点D，E；分别以D，E为圆心，以大于

  1

  2

  DE

  的长为半径作弧，两弧在∠BAC内交于点F，作射线AF交BC于点G．若AB=8，且△ABG的面积为10，则CG的长为

  ．
  组卷：386引用：3难度：0.6

  解析

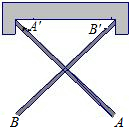• 11．如图，把两根钢条AA′、BB′的中点连在一起，可以做成一个测量工件内槽宽的工具（卡钳），若测得AB=5米，则槽宽为

   

  米．
  组卷：553引用：13难度：0.7

  解析

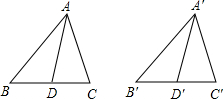• 12．如图，AD、A′D′分别是锐角三角形ABC和锐角三角形A′B′C′中∠BAC和∠B′A′C′的平分线，且AB=A′B′，AD=A′D′，若使△ABC≌△A′B′C′，请你补充条件

  ．（填写一个你认为适当的条件即可）
  组卷：42引用：2难度：0.5

  解析

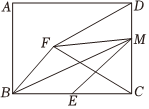• 13．如图，矩形ABCD中，AB=3，BC=4，E是BC中点，CD上有一动点M，连接EM、BM，将△BEM沿着BM翻折得到△BFM，连接DF，CF，则DF+

  1

  2

  CF的最小值为

  ．
  组卷：167引用：1难度：0.4

  解析

• 14．已知点P₁（a-1，5）和点P₂（2，b-1）关于x轴对称，则（a+b）²⁰⁰⁵=

   

  ．
  组卷：251引用：5难度：0.9

  解析

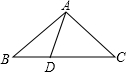• 15．如图，在△ABC中，D为BC上的一点，AB=AC=DC，AD=BD，则∠BAC=

   

  度．
  组卷：53引用：16难度：0.7

  解析

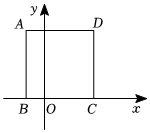• 16．如图，正方形ABCD的顶点B、C都在x轴上，若点A的坐标是（-1，4），点B的坐标是（-1，0），则点C的坐标是

  ．
  组卷：341引用：4难度：0.6

  解析

三、解答题（共52分，第17-24题，每题5分，第25-26题，每题6分）

• 17．如图，在△ABC中，AB=AC，AB的垂直平分线交AB于点N，交BC的延长线于点M，若∠A=40°．
  （1）求∠NMB的度数；
  （2）如果将（1）中∠A的度数改为70°，其余条件不变，再求∠NMB的度数；
  （3）你发现有什么样的规律性，试证明之．
  组卷：173引用：6难度：0.5

  解析

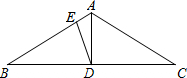• 18．△ABC中，AB=AC，∠BAC=120°，AD是BC边上的中线，且BD=BE，求∠AED的度数．
  组卷：78引用：1难度：0.3

  解析

• 19．阅读下面材料，再回答问题：
  有一些几何图形可以被某条直线分成面积相等的两部分，我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”，如三角形的中线所在的直线一定是三角形的“二分线”．
  解决下列问题：
  （1）在图1中，试用三种不同的方法分别画出平行四边形ABCD的“二分线”．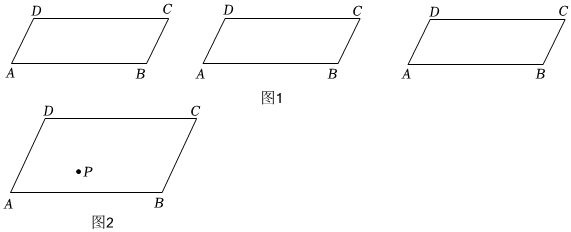
  
  （2）由上述方法，你能得到什么一般性的结论？
  （3）解决问题：有一块平行四边形田地ABCD，现要修一条笔直的小路（路的宽度不计把它分成面积相等的两块种植两种不同的花卉，由于在这块地里有一个凉亭P（大小不计），如图2所示，为了方便使得所修的路经过凉亭P，聪明的你能帮他们解决这个问题吗？（画图，并说明画法）
  组卷：34引用：1难度：0.5

  解析

• 20．如图，BD∥AC，BD=BC，点E在BC上，且BE=AC．求证：∠D=∠ABC．
  组卷：2586引用：26难度：0.7

  解析

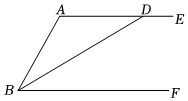• 21．已知：如图，AE∥BF，BD平分∠ABC，且交AE于点D．
  （1）尺规作图：作射线AC平分∠BAD，且交BF于点C（保留作图痕迹）；
  （2）连接CD，请判断四边形ABCD是什么四边形？并证明．
  组卷：9引用：1难度：0.5

  解析

• 22．已知：如图，在△ABC中，∠ACB=90°，点D是边AB的中点，DE∥BC，BE∥CD，连接AE、CE．
  （1）求证：△ADE≌△CDE；
  （2）如果CE平分∠ACB，求证：AC=3BC．
  组卷：211引用：1难度：0.4

  解析

• 23．已知AB=BC，∠ABC=90°，直线l是过点B的一条动直线（不与直线AB，BC重合），分别过点A，C作直线l的垂线，垂足为D，E．
  （1）如图1，当45°＜∠ABD＜90°时，
  ①求证：CE+DE=AD；
  ②连接AE，过点D作DH⊥AE于H，过点A作AF∥BC交DH的延长线于点F．依题意补全图形，用等式表示线段DF，BE，DE的数量关系，并证明；
  （2）在直线l运动的过程中，若DE的最大值为3，直接写出AB的长．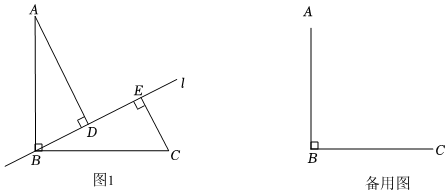
  
  组卷：1421引用：5难度：0.4

  解析

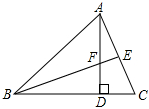• 24．如图△ABC中，AD⊥BC于D，若BD=AD，FD=CD．
  （1）求证：∠FBD=∠CAD；
  （2）∠BEC=

  °．
  组卷：47引用：1难度：0.5

  解析

• 25．（1）如图1，∠MAN=90°，射线AD在这个角的内部，点B、C分别在∠MAN的边AM、AN上，且AB=AC，CF⊥AD于点F，BE⊥AD于点E．求证：BE=AF
  （2）如图2，点B、C分别在∠MAN的边AM、AN上，点E、F都在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC，且∠1=∠2=∠BAC．（1）中结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．
  （3）如图3，在△ABC中，AB=AC，AB＞BC．点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC．若△ABC的面积为15，求△ACF与△BDE的面积之和．
  
  组卷：438引用：3难度：0.1

  解析

• 26．如图，在网格中，每一个小正方形的边长都为1，点A，B，C，M，N都在格点上．
  （1）作△ABC关于直线MN的轴对称图形△ADE；
  （2）设BC与DE交于点F，连接BE，CD，得到一个凹六边形ABEFCD，求该凹六边形的面积．
  组卷：6引用：1难度：0.5

  解析