当前位置：试卷中心 > 试卷详情

2020-2021学年天津市河西区七年级（下）期末数学试卷

发布：2025/8/18 2:0:5

一、选择题:本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的

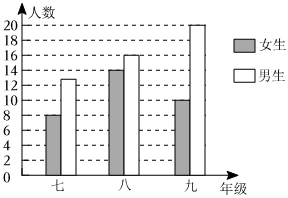1．从如图所示的统计图中，我们可以得到一些信息，下面是某同学通过读图得到的一些信息，其中正确的信息是（　　）
A．八年级的学生比九年级的学生多
B．九年级的男生人数是女生人数的2倍
C．三个年级女生共有30人
D．三个年级男生总数比女生总数多15人
组卷：11引用：1难度：0.7
2．已知43²=1849，44²=1936，45²=2025，46²=2116．若n为整数且n＜
2021
＜n+1，则n的值为（　　）
A．43 B．44 C．45 D．46
组卷：2924引用：26难度：0.8
3．我国古代《孙子算经》记载“多人共车”问题：“今有三人共车，二车空；二人共车，九人步，问人与车各几何？”意思是说：“每三人共乘一辆车，最终剩余2辆车；每2人共乘一辆车，最终有9人无车可乘，问人和车的数量各是多少？”下面四个同学的思考正确的是（　　）
小聪：设共有x人，根据题意得：
x
3
-
2
=
x
-
9
2
；
小明：设共有x人，根据题意得：
x
3
+
2
=
x
-
9
2
；
小玲：设共有车y辆，根据题意得：3（y-2）=2y+9；
小丽：设共有车y辆，根据题意得：3（y+2）=2y+9．
A．小聪、小丽 B．小聪、小明 C．小明、小玲 D．小明、小丽
组卷：424引用：5难度：0.7
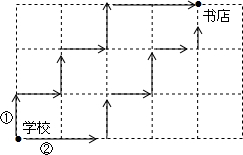4．如图，从学校到书店有两条路可走，请你判断下列说法正确的是（　　）
A．路①近 B．路②近 C．一样近 D．无法确定
组卷：100引用：2难度：0.9
5．当0＜x＜1时，x,
1
x
，x²的大小顺序是（　　）
A．
1
x
＜x＜x² B．x＜x²＜
1
x
C．x²＜x＜
1
x
D．
1
x
＜x²＜x
组卷：8018引用：66难度：0.9
6．已知x=4是关于x的方程kx+b=0（k≠0，b＞0）的解，则关于x的不等式k（x-3）+2b＞0的解集是（　　）
A．x＞11 B．x＜11 C．x＞7 D．x＜7
组卷：3939引用：11难度：0.5
7．如图，AC⊥BC，AC=4.5，若点P在直线BC上，则AP的长可能是（　　）
A．5 B．4 C．3 D．2
组卷：1114引用：13难度：0.6
8．滨州市教育局为了了解实行课改后七年级学生在家的学习时间，应采用的最佳调查方式是（　　）
A．对所有学校进行全面调查
B．抽取农村和城区部分学校进行调查
C．只对一所学校进行调查
D．只对城区学校进行调查
组卷：83引用：14难度：0.9
9．在平面直角坐标系中，把点A（1，3）向右平移3个单位长度，得到的点B的坐标为（　　）
A．（1，6） B．（1，0） C．（4，3） D．（-2，3）
组卷：102引用：3难度：0.8
10．在平面直角坐标系中，点
P
（
2
，-
3
）
在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
组卷：12引用：2难度：0.8

二、填空题:本大题共6小题,每小题3分,共18分,请将答案直接填在题中横线上.

11．某学校医务室采购了一批水银温度计和额温枪，其中有10支水银温度计，若干支额温枪．已知水银温度计每支5元，额温枪每支230元，如果总费用不超过1000元，那么额温枪至多有
支．
组卷：171引用：1难度：0.7
12．若三个连续正整数的和小于9，则这三个连续的正整数
．
组卷：47引用：1难度：0.9
13．若二元一次方程组
x
+
2
y
=
m
+
3
x
+
y
=
2
m
的解x,y的值恰好是一个等腰三角形两边的长，且这个等腰三角形的周长为7，则m的值为
．
组卷：2019引用：29难度：0.9
14．4的平方根是
，27的立方根是
．
组卷：376引用：4难度：0.7
15．如图，正方形ABCD中，点E、F分别在边BC、CD上，且AE=EF=FA．下列结论：①△ABE≌△ADF；②CE=CF；③∠AEB=75°；④BE+DF=EF；⑤S_△ABE+S_△ADF=S_△CEF，其中正确的是
（只填写序号）．
组卷：2562引用：25难度：0.5
16．学校要从甲、乙中选拔1人参加运动会志愿者工作，选拔项目为普通话、体育知识和旅游知识，并将成绩依次按2：1：2记分．两人的各项选拔成绩如表所示，则最终胜出的同学是
．

普通话体育知识旅游知识

甲 8 9 7

乙 9 8 7

组卷：25引用：1难度：0.7

三、解答题:本大题共7小题,共52分.解答应写出文字说明、演算步骤或证明过程.

17．某市电信局现有600部已申请装机的固定电话尚待装机，此外每天还有新申请装机的电话也待装机，设每天新申请装机的固定电话部数相同，每个电话装机小组每天安装的固定电话部数也相同，若安排3个装机小组，恰好60天可将待装固定电话装机完毕；若安排5个装机小组，恰好20天可将待装固定电话装机完毕．求每天新申请装机的固定电话部数和每个电话装机小组每天安装的固定电话部数．
组卷：203引用：2难度：0.5
18．重庆市教委想把长跑作为中考考查项目，在此之前做了一个调查，来了解我市体育长跑的得分情况，从甲、乙两所学校各随机抽取了20名学生的学生成绩如下．（该项满分10分，学生得分均为整数）．甲学校20名学生成绩（单位：分）分别为：
7，7，8，9，8，6，7，8，8，10，7，9，6，8，7，8，9，7，8，9
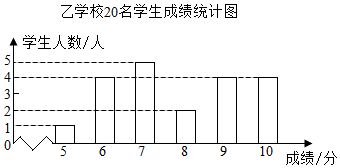
乙学校20名学生成绩的条形统计图如图所示：
经过对两校这20名学生成绩的整理，得到分析数据如下表：

组别极差平均分中位数方差

甲 a 7.8 8 1.05

乙 5 b c 2.46

（1）求出表中的a、b、c的值．
（2）长跑得分9分及其以上即为优秀，已知甲学校有1800人，请估算甲学校的优秀人数有多少人？
（3）根据以上数据，你觉得甲、乙两所学校的学生哪所学校长跑比较好？请说明理由（一条即可）．
组卷：14引用：1难度：0.7
19．思维启迪：
（1）如图1，点P是线段AB，CD的中点，则AC与BD的数量关系为
，位置关系为
；
思维探索：
（2）①如图2，在△ABC中，∠ACB=90°，点D为△ABC内一点，连接BD，DC，延长DC到点E，使CE=CD，连接AE，若BD⊥AE，请用等式表示AB，BD，AE之间的数量关系，并说明理由；
②如图3，在△ABC中，∠ACB=90°，AC=BC，点D为AB中点，点E在线段BD上（点E不与点B，点D重合），连接CE，过点A作AF⊥CE，连接FD．若AF=8，CF=3，请直接写出FD的长．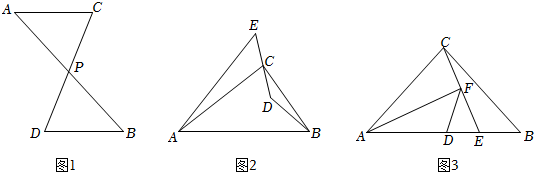
组卷：1348引用：8难度：0.1
20．【学习新知】射到平面镜上的光线（入射光线）和反射后的光线（反射光线）与平面镜所夹的角相等．如图1，AB是平面镜，若入射光线与水平镜面夹角为∠1，反射光线与水平镜面夹角为∠2，则∠1=∠2．
（1）【初步应用】如图2，一束光线m射到平面镜a上，被a反射到平面镜b上，又被b反射，若被b反射出的光线n与光线m平行，且∠1=50°，则∠2=
，∠3=
．
（2）【猜想验证】由（1），请你猜想：当两平面镜a、b的夹角∠3=
　时，可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后，入射光线m与反射光线n平行．请说明理由．
（3）【拓展探究】如图3，有三块平面镜AB，BC，CD，入射光线EF与镜面AB的夹角∠1=α°，镜面AB、BC的夹角∠B=120°，已知入射光线从镜面AB开始反射，经过n（n为正整数，n≤3）次反射，当第n次反射光线与入射光线EF平行时，请直接写出∠BCD的度数．（可用含有α的代数式表示）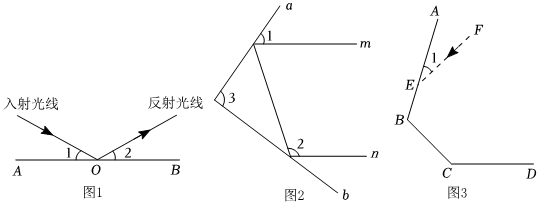
组卷：811引用：2难度：0.5
21．解不等式组
7
x
-
1
≤
3
+
9
x
x
-
x
+
2
2
＜
2
-
x
3
，并把它们的解在数轴上表示出来．
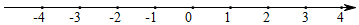组卷：2187引用：5难度：0.5
22．解方程组
4
（
y
-
x
-
1
）
=
3
（
1
-
x
）
-
2
x
3
+
y
2
=
2
．
组卷：213引用：2难度：0.8
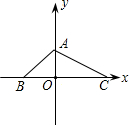23．已知，如图，在平面直角坐标系中，S_△ABC=24，OA=OB，BC=12，求△ABC三个顶点的坐标．
组卷：585引用：25难度：0.3

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

	普通话	体育知识	旅游知识
甲	8	9	7
乙	9	8	7

组别	极差	平均分	中位数	方差
甲	a	7.8	8	1.05
乙	5	b	c	2.46

2020-2021学年天津市河西区七年级（下）期末数学试卷

一、选择题:本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的

1．从如图所示的统计图中，我们可以得到一些信息，下面是某同学通过读图得到的一些信息，其中正确的信息是（ ）

2．已知432=1849，442=1936，452=2025，462=2116．若n为整数且n＜2021＜n+1，则n的值为（ ）

4．如图，从学校到书店有两条路可走，请你判断下列说法正确的是（ ）

5．当0＜x＜1时，x,1x，x2的大小顺序是（ ）

6．已知x=4是关于x的方程kx+b=0（k≠0，b＞0）的解，则关于x的不等式k（x-3）+2b＞0的解集是（ ）

7．如图，AC⊥BC，AC=4.5，若点P在直线BC上，则AP的长可能是（ ）

8．滨州市教育局为了了解实行课改后七年级学生在家的学习时间，应采用的最佳调查方式是（ ）

9．在平面直角坐标系中，把点A（1，3）向右平移3个单位长度，得到的点B的坐标为（ ）

10．在平面直角坐标系中，点P（2，-3）在（ ）

二、填空题:本大题共6小题,每小题3分,共18分,请将答案直接填在题中横线上.

11．某学校医务室采购了一批水银温度计和额温枪，其中有10支水银温度计，若干支额温枪．已知水银温度计每支5元，额温枪每支230元，如果总费用不超过1000元，那么额温枪至多有 支．

12．若三个连续正整数的和小于9，则这三个连续的正整数 ．

13．若二元一次方程组x+2y=m+3x+y=2m的解x,y的值恰好是一个等腰三角形两边的长，且这个等腰三角形的周长为7，则m的值为 ．

14．4的平方根是 ，27的立方根是 ．

15．如图，正方形ABCD中，点E、F分别在边BC、CD上，且AE=EF=FA．下列结论：①△ABE≌△ADF；②CE=CF；③∠AEB=75°；④BE+DF=EF；⑤S△ABE+S△ADF=S△CEF，其中正确的是（只填写序号）．

16．学校要从甲、乙中选拔1人参加运动会志愿者工作，选拔项目为普通话、体育知识和旅游知识，并将成绩依次按2：1：2记分．两人的各项选拔成绩如表所示，则最终胜出的同学是 ． 普通话 体育知识 旅游知识 甲 8 9 7 乙 9 8 7

三、解答题:本大题共7小题,共52分.解答应写出文字说明、演算步骤或证明过程.

21．解不等式组7x-1≤3+9xx-x+22＜2-x3，并把它们的解在数轴上表示出来．

22．解方程组4（y-x-1）=3（1-x）-2x3+y2=2．

23．已知，如图，在平面直角坐标系中，S△ABC=24，OA=OB，BC=12，求△ABC三个顶点的坐标．

1．从如图所示的统计图中，我们可以得到一些信息，下面是某同学通过读图得到的一些信息，其中正确的信息是（　　）

2．已知43²=1849，44²=1936，45²=2025，46²=2116．若n为整数且n＜
2021
＜n+1，则n的值为（　　）

4．如图，从学校到书店有两条路可走，请你判断下列说法正确的是（　　）

5．当0＜x＜1时，x,
1
x
，x²的大小顺序是（　　）

6．已知x=4是关于x的方程kx+b=0（k≠0，b＞0）的解，则关于x的不等式k（x-3）+2b＞0的解集是（　　）

7．如图，AC⊥BC，AC=4.5，若点P在直线BC上，则AP的长可能是（　　）

8．滨州市教育局为了了解实行课改后七年级学生在家的学习时间，应采用的最佳调查方式是（　　）

9．在平面直角坐标系中，把点A（1，3）向右平移3个单位长度，得到的点B的坐标为（　　）

10．在平面直角坐标系中，点
P
（
2
，-
3
）
在（　　）

11．某学校医务室采购了一批水银温度计和额温枪，其中有10支水银温度计，若干支额温枪．已知水银温度计每支5元，额温枪每支230元，如果总费用不超过1000元，那么额温枪至多有
支．

12．若三个连续正整数的和小于9，则这三个连续的正整数
．

13．若二元一次方程组
x
+
2
y
=
m
+
3
x
+
y
=
2
m
的解x,y的值恰好是一个等腰三角形两边的长，且这个等腰三角形的周长为7，则m的值为
．

14．4的平方根是
，27的立方根是
．

15．如图，正方形ABCD中，点E、F分别在边BC、CD上，且AE=EF=FA．下列结论：①△ABE≌△ADF；②CE=CF；③∠AEB=75°；④BE+DF=EF；⑤S_△ABE+S_△ADF=S_△CEF，其中正确的是
（只填写序号）．

16．学校要从甲、乙中选拔1人参加运动会志愿者工作，选拔项目为普通话、体育知识和旅游知识，并将成绩依次按2：1：2记分．两人的各项选拔成绩如表所示，则最终胜出的同学是
．

普通话体育知识旅游知识

甲 8 9 7

乙 9 8 7

21．解不等式组
7
x
-
1
≤
3
+
9
x
x
-
x
+
2
2
＜
2
-
x
3
，并把它们的解在数轴上表示出来．

22．解方程组
4
（
y
-
x
-
1
）
=
3
（
1
-
x
）
-
2
x
3
+
y
2
=
2
．

23．已知，如图，在平面直角坐标系中，S_△ABC=24，OA=OB，BC=12，求△ABC三个顶点的坐标．