当前位置：试卷中心 > 试卷详情

2024-2025学年山西省忻州市三校联考八年级（上）期末数学试卷

发布：2025/8/1 20:0:5

一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项符合题目要求）

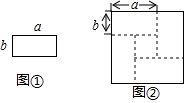1．小张利用如图①所示的长为a、宽为b的长方形卡片4张，拼成了如图②所示的图形，则根据图②的面积关系能验证的恒等式为（　　）
A．（a+b）²=a²+2ab+b² B．（2a+b）²=4a²+4ab+b²
C．（a+b）²=（a-b）²+4ab D．（a-b）²=a²-2ab+b²
组卷：1652引用：6难度：0.7
2．如图所示，在△ABC中，AB=AC，BE=CE，则由“SSS”可以判定（　　）
A．△ABD≌△ACD B．△BDE≌△CDE C．△ABE≌△ACE D．以上都不对
组卷：769引用：19难度：0.9
3．下列各式中，计算结果是a⁶的是（　　）
A．a⁶-a⁰ B．a¹²÷a² C．a³•a² D．（a²）³
组卷：59引用：3难度：0.8
4．1纳米=0.000 000 001米，则2.5纳米应表示为（　　）米．
A．2.5×10^-8 B．2.5×10^-9 C．2.5×10^-10 D．2.5×10⁹
组卷：99引用：8难度：0.9
5．已知一个多边形的内角和是外角和的
3
2
，则这个多边形的边数是（　　）
A．4 B．5 C．6 D．7
组卷：828引用：3难度：0.9
6．某校1993名学生参加运动会，学校买了1993瓶汽水供应每一个学生一瓶，商店规定，每7个空瓶可换一瓶汽水，因此，同学们每喝完7瓶汽水就换回一瓶汽水，这样，他们最多能喝（　　）瓶汽水．
A．1993 B．2325 C．2324 D．1994
组卷：41引用：1难度：0.7
7．在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是（　　）
A． B． C． D．
组卷：151引用：2难度：0.8
8．施工队铺设3000米的下水管道，每天比原计划少施工50米，结果延期4天完成任务．设原计划每天施工x米，所列方程正确的是（　　）
A．
3000
x
-
3000
x
+
50
=
4
B．
3000
x
-
50
-
3000
x
=
4
C．
3000
x
-
3000
x
-
50
=
4
D．
3000
x
+
50
-
3000
x
=
4
组卷：296引用：5难度：0.7
9．已知：如图，在△ABC中，AD是∠BAC的平分线，E为AD上一点，且EF⊥BC于点F．若∠C=35°，∠DEF=15°，则∠B的度数为（　　）
A．60° B．65° C．75° D．85°
组卷：1326引用：11难度：0.7
10．如图，OP平分∠AOB，PA⊥OA，PB⊥OB，垂足分别为A，B．下列结论中不一定成立的是（　　）
A．PA=PB B．PO平分∠APB
C．OA=OB D．AB垂直平分OP
组卷：3568引用：161难度：0.7

二、填空题（共5小题，每小题3分，共15分）

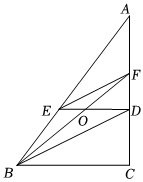11．如图，BD平分∠ABC交AC于点D，过点D作DE∥BC交AB于点E，EF平分∠AED交AC于点F，连接BF交DE于点O．有下列四个结论：①EF∥BD；②∠AEF=∠EDB；③∠ABF=∠DBF；④S_△EOB=S_△FOD．
其中结论正确的有
.（写出全部正确结论序号）
组卷：84引用：1难度：0.5
12．化简：
3
m
2
n
9
m
=
．
组卷：994引用：7难度：0.8
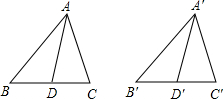13．如图，AD、A′D′分别是锐角三角形ABC和锐角三角形A′B′C′中∠BAC和∠B′A′C′的平分线，且AB=A′B′，AD=A′D′，若使△ABC≌△A′B′C′，请你补充条件
．（填写一个你认为适当的条件即可）
组卷：42引用：2难度：0.5
14．要使分式
2
x
-
1
有意义，则x的取值范围为
．
组卷：384引用：14难度：0.8
15．分解因式：（
）²+20xy+25y²=（
）²．
组卷：58引用：4难度：0.7

三、解答题（本大题共8小题，共75分．解答应写出文字说明，证明过程或演算步骤）

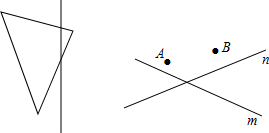16．（1）以直线为对称轴，画出下列图形的另一部分使它们成为轴对称图形．
（2）如图，求作点P，使点P同时满足：①PA=PB；②到直线m,n的距离相等．（尺规作图，保留作图痕迹）
组卷：49引用：1难度：0.5
17．某商厦进货员预测一种应季衬衫能畅销市场，就用1.2万元购进这种衬衫，面市后果然供不应求．于是，商厦又用2.64万元购进了第二批这种衬衫，所购数量是第一批购进数量的2倍，但单价贵了6元，商厦销售这种衬衫时每件预定售价都是87元．
（1）求这种衬衫原进价为每件多少元？
（2）经过一段时间销售，根据市场饱和情况，为了提高回款速度，商厦经理决定对剩余的100件衬衫打5折销售，请你求一下销售完这两批衬衫商厦获得的总利润．
组卷：131引用：2难度：0.7
18．已知：如图①，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=50°．
（1）①求证：AC=BD；
②∠APB=
；
（2）如图②，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=α，则AC与BD间的等量关系为
，∠APB的大小为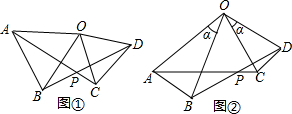
．
组卷：35引用：1难度：0.5
19．将纸片△ABC沿DE折叠使点A落在A′处的位置．

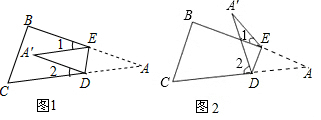
（1）如果A′落在四边形BCDE的内部（如图1），∠A′与∠1+∠2之间存在怎样的数量关系？并说明理由．
（2）如果A′落在四边形BCDE的BE边上，这时图1中的∠1变为0°角，则∠A′与∠2之间的关系是
．
（3）如果A′落在四边形BCDE的外部（如图2），这时∠A′与∠1、∠2之间又存在怎样的数量关系？并说明理由．
组卷：5269引用：12难度：0.5
20．如图，已知D、E分别是AB、AC的中点，AB=AC，求证：∠B=∠C．
组卷：273引用：2难度：0.7
21．先化简，再求值：
（
1
-
1
x
+
3
）
÷
x
2
-
4
x
+
3
，其中x=1．
组卷：277引用：2难度：0.7
22．因式分解：
（1）2x³-4x²y+2xy²；
（2）（m+n）（m+n-4）+4[提示：把m+n看成一个整体]．
组卷：33引用：2难度：0.8
23．阅读下面的材料：
【材料一】若m²-2mn+2n²-8n+16=0，求m,n的值．
解：∵m²-2mn+2n²-8n+16=0，
∴（m²-2mn+n²）+（n²-8n+16）=0，
∴（m-n）²+（n-4）²=0，
∴（m-n）²=0，（n-4）²=0，
∴n=4，m=4．
【材料二】“a≥0”这个结论在数学中非常有用，有时我们需要将代数式配成完全平方式．例如：m²+8m+17=m²+8m+16+1=（m+4）²+1．
∵（m+4）²≥0，
∴（m+4）²+1≥1，
∴m²+8m+17≥1．
故m²+8m+17有一个最小值为1．
阅读材料，探究下列问题：
（1）已知x²-2xy+2y²+6y+9=0，求xy的值；
（2）无论m取何值，代数式m²+6m+13总有一个最小值，求出它的最小值．
组卷：409引用：4难度：0.7

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．（a+b）²=a²+2ab+b²	B．（2a+b）²=4a²+4ab+b²
C．（a+b）²=（a-b）²+4ab	D．（a-b）²=a²-2ab+b²

A． 3000 x - 3000 x + 50 = 4	B． 3000 x - 50 - 3000 x = 4
C． 3000 x - 3000 x - 50 = 4	D． 3000 x + 50 - 3000 x = 4

A．PA=PB	B．PO平分∠APB
C．OA=OB	D．AB垂直平分OP

2024-2025学年山西省忻州市三校联考八年级（上）期末数学试卷

一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项符合题目要求）

1．小张利用如图①所示的长为a、宽为b的长方形卡片4张，拼成了如图②所示的图形，则根据图②的面积关系能验证的恒等式为（ ）

2．如图所示，在△ABC中，AB=AC，BE=CE，则由“SSS”可以判定（ ）

3．下列各式中，计算结果是a6的是（ ）

4．1纳米=0.000 000 001米，则2.5纳米应表示为（ ）米．

5．已知一个多边形的内角和是外角和的32，则这个多边形的边数是（ ）

6．某校1993名学生参加运动会，学校买了1993瓶汽水供应每一个学生一瓶，商店规定，每7个空瓶可换一瓶汽水，因此，同学们每喝完7瓶汽水就换回一瓶汽水，这样，他们最多能喝（ ）瓶汽水．

7．在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是（ ）

8．施工队铺设3000米的下水管道，每天比原计划少施工50米，结果延期4天完成任务．设原计划每天施工x米，所列方程正确的是（ ）

9．已知：如图，在△ABC中，AD是∠BAC的平分线，E为AD上一点，且EF⊥BC于点F．若∠C=35°，∠DEF=15°，则∠B的度数为（ ）

10．如图，OP平分∠AOB，PA⊥OA，PB⊥OB，垂足分别为A，B．下列结论中不一定成立的是（ ）

二、填空题（共5小题，每小题3分，共15分）

11．如图，BD平分∠ABC交AC于点D，过点D作DE∥BC交AB于点E，EF平分∠AED交AC于点F，连接BF交DE于点O．有下列四个结论：①EF∥BD；②∠AEF=∠EDB；③∠ABF=∠DBF；④S△EOB=S△FOD．其中结论正确的有 .（写出全部正确结论序号）

12．化简：3m2n9m=．

13．如图，AD、A′D′分别是锐角三角形ABC和锐角三角形A′B′C′中∠BAC和∠B′A′C′的平分线，且AB=A′B′，AD=A′D′，若使△ABC≌△A′B′C′，请你补充条件．（填写一个你认为适当的条件即可）

14．要使分式2x-1有意义，则x的取值范围为 ．

15．分解因式：（）2+20xy+25y2=（）2．

三、解答题（本大题共8小题，共75分．解答应写出文字说明，证明过程或演算步骤）

16．（1）以直线为对称轴，画出下列图形的另一部分使它们成为轴对称图形．（2）如图，求作点P，使点P同时满足：①PA=PB；②到直线m,n的距离相等．（尺规作图，保留作图痕迹）

18．已知：如图①，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=50°．（1）①求证：AC=BD；②∠APB=；（2）如图②，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=α，则AC与BD间的等量关系为，∠APB的大小为．

20．如图，已知D、E分别是AB、AC的中点，AB=AC，求证：∠B=∠C．

21．先化简，再求值：（1-1x+3）÷x2-4x+3，其中x=1．

22．因式分解：（1）2x3-4x2y+2xy2；（2）（m+n）（m+n-4）+4[提示：把m+n看成一个整体]．

1．小张利用如图①所示的长为a、宽为b的长方形卡片4张，拼成了如图②所示的图形，则根据图②的面积关系能验证的恒等式为（　　）

2．如图所示，在△ABC中，AB=AC，BE=CE，则由“SSS”可以判定（　　）

3．下列各式中，计算结果是a⁶的是（　　）

4．1纳米=0.000 000 001米，则2.5纳米应表示为（　　）米．

5．已知一个多边形的内角和是外角和的
3
2
，则这个多边形的边数是（　　）

6．某校1993名学生参加运动会，学校买了1993瓶汽水供应每一个学生一瓶，商店规定，每7个空瓶可换一瓶汽水，因此，同学们每喝完7瓶汽水就换回一瓶汽水，这样，他们最多能喝（　　）瓶汽水．

7．在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是（　　）

8．施工队铺设3000米的下水管道，每天比原计划少施工50米，结果延期4天完成任务．设原计划每天施工x米，所列方程正确的是（　　）

9．已知：如图，在△ABC中，AD是∠BAC的平分线，E为AD上一点，且EF⊥BC于点F．若∠C=35°，∠DEF=15°，则∠B的度数为（　　）

10．如图，OP平分∠AOB，PA⊥OA，PB⊥OB，垂足分别为A，B．下列结论中不一定成立的是（　　）

11．如图，BD平分∠ABC交AC于点D，过点D作DE∥BC交AB于点E，EF平分∠AED交AC于点F，连接BF交DE于点O．有下列四个结论：①EF∥BD；②∠AEF=∠EDB；③∠ABF=∠DBF；④S_△EOB=S_△FOD．
其中结论正确的有
.（写出全部正确结论序号）

12．化简：
3
m
2
n
9
m
=
．

13．如图，AD、A′D′分别是锐角三角形ABC和锐角三角形A′B′C′中∠BAC和∠B′A′C′的平分线，且AB=A′B′，AD=A′D′，若使△ABC≌△A′B′C′，请你补充条件
．（填写一个你认为适当的条件即可）

14．要使分式
2
x
-
1
有意义，则x的取值范围为
．

15．分解因式：（
）²+20xy+25y²=（
）²．

16．（1）以直线为对称轴，画出下列图形的另一部分使它们成为轴对称图形．
（2）如图，求作点P，使点P同时满足：①PA=PB；②到直线m,n的距离相等．（尺规作图，保留作图痕迹）

18．已知：如图①，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=50°．
（1）①求证：AC=BD；
②∠APB=
；
（2）如图②，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=α，则AC与BD间的等量关系为
，∠APB的大小为
．

21．先化简，再求值：
（
1
-
1
x
+
3
）
÷
x
2
-
4
x
+
3
，其中x=1．

22．因式分解：
（1）2x³-4x²y+2xy²；
（2）（m+n）（m+n-4）+4[提示：把m+n看成一个整体]．