当前位置：试卷中心 > 试卷详情

2023-2024学年北京市朝阳区陈经纶中学八年级（下）月考数学试卷（3月份）

发布：2025/7/29 3:0:19

一、单选题

1．现已知线段a,b（a＜b），∠MON=90°，求作Rt△ABO，使得∠O=90°，OA=a,AB=b.小惠和小雷的作法分别如下：
小惠：①以点O为圆心、线段a的长为半径画弧，交射线ON于点A；②以点A为圆心、线段b的长为半径画弧，交射线OM于点B，连接AB，△ABO即为所求．
小雷：①以点O为圆心、线段a的长为半径画弧，交射线ON于点A；②以点O为圆心、线段b的长为半径画弧，交射线OM于点B，连接AB，△ABO即为所求．
则下列说法中正确的是（　　）
A．小惠的作法正确，小雷的作法错误
B．小雷的作法正确，小惠的作法错误
C．两人的作法都正确
D．两人的作法都错误
组卷：35引用：5难度：0.5
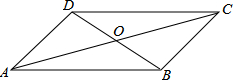2．四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（　　）
A．AB∥DC，AD∥BC B．AB=DC，AD=BC
C．AO=CO，BO=DO D．AB∥DC，AD=BC
组卷：3425引用：151难度：0.9
3．已知a为整数，且
3
50
＜
a
+
2
＜
18
，则a的值为（　　）
A．3 B．2 C．1 D．0
组卷：149引用：3难度：0.9
4．已知△ABC中，a、b、c分别是∠A、∠B、∠C的对边，下列条件中不能判断△ABC是直角三角形的是（　　）
A．∠A：∠B：∠C=3：4：5 B．∠C=∠A-∠B
C．a²-b²=c² D．a：b：c=7：24：25
组卷：529引用：9难度：0.5
5．小华先向东走了16m后，接着向北走了12m,此时小华离出发点的距离是（　　）
A．28 m B．16 m C．20 m D．12 m
组卷：135引用：1难度：0.7
6．下列计算错误的是（　　）
A．
2
×
5
=
10
B．
2
+
5
=
7
C．
18
÷
2
=
3
D．
12
=
2
3
组卷：579引用：26难度：0.7
7．在△ABC中，∠C=90°，AC=8，BC=6，则AB的长为（　　）
A．5 B．10 C．
2
7
D．28
组卷：1009引用：9难度：0.9
8．下列二次根式中，最简二次根式是（　　）
A．
42
B．
12
C．
1
3
D．
0
.
1
组卷：201引用：2难度：0.9
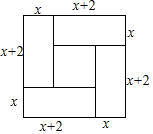9．如图所示，把四个长和宽分别为x+2和x的矩形拼接成大正方形．若四个矩形和中间小正方形的面积和为4×35+2²，则根据题意能列出的方程是（　　）
A．x²+2x-35=0 B．x²+2x+35=0 C．x²+2x-4=0 D．x²+2x+4=0
组卷：652引用：2难度：0.9
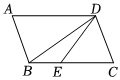10．如图，在平行四边形ABCD中，∠ABC=110°，BD=BC，点E在BC上，∠BDE=20°，则∠DEC的度数为（　　）
A．50° B．60° C．70° D．80°
组卷：79引用：1难度：0.6

二、填空题

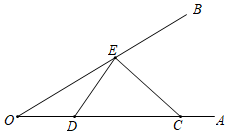11．如图，∠AOB=30°，点C、D均在射线OA上，且OC=6，OD=2，点E为射线OB上一动点，则CE+DE的最小值为
．
组卷：940引用：2难度：0.6
12．直角三角形一直角边为5厘米、斜边为13厘米，那么斜边上的高是

．
组卷：55引用：1难度：0.5
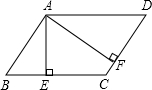13．如图所示，在▱ABCD中，AE⊥BC于E，AF⊥CD于F，∠BAD=120°，BE=2，FD=3，则∠EAF=
，▱ABCD的周长为
．
组卷：65引用：1难度：0.9
14．函数y=
1
x
-
2021
自变量x的取值范围是
．
组卷：466引用：6难度：0.8
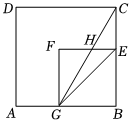15．如图，正方形ABCD的面积为5，正方形BEFG面积为4，那么△GCE的面积是
．
组卷：465引用：9难度：0.7
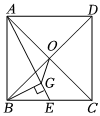16．正方形ABCD的边长为4，点E是BC的中点，过点B作BG⊥AE，垂足为G，O为对角线AC、BD的交点，连接OG，则OG=
．
组卷：211引用：3难度：0.6

三、解答题

17．小明家有一块长方形的地，它的长为
2
3
m
，宽为
6
m,则这块地的面积是多少？
组卷：10引用：2难度：0.9
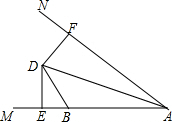18．如图，D是∠MAN内部一点，点B是射线AM上一点，DE⊥AM于E，DF⊥AN于F，且DE=DF，连接AD．
（1）求证：AD平分∠MAN；（可不用全等）
（2）在射线AN上取一点C，使得DC=DB，若AB=6，BE=2，则AC长为

．
组卷：159引用：1难度：0.3
19．对于任意不相等的两个数a,b,定义一种运算※如下：a※b=
a
+
b
a
-
b
，如3※2=
3
+
2
3
-
2
=
5
．试求12※4的值．
组卷：167引用：1难度：0.3
20．阅读材料：黑白双雄，纵横江湖，双剑合璧，天下无敌，这是武侠小说中的常见描述，其意指两个人合在一起，取长补短，威力无比．在二次根式中也有这样相辅相成的例子．
如（2+
3
）（2-
3
）=2²-（-
3
）²=1，（
5
+
2
）（
5
-
2
）=（
5
）²-（
2
）²=3，它们的积是有理数，我们说这两个二次根式互为有理化因式，其中一个是另一个的有理数因式．于是，我们可以将下面的式子化简：
1
2
-
3
=
2
+
3
（
2
-
3
）
（
2
+
3
）
=2+
3

解决问题：
（1）4+
7
的一个有理化因式是
．
（2）计算：
1
3
+
1
+
1
5
+
3
+
1
7
+
5
+…+
1
2017
+
2015
．
组卷：109引用：1难度：0.3
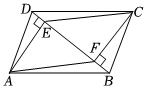21．如图，在▱ABCD中，分别过A，C两点作对角线BD的垂线，垂足分别为E，F．
求证：四边形AFCE是平行四边形．
组卷：252引用：3难度：0.5
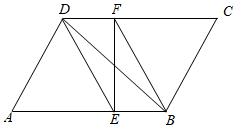22．已知：如图所示，在平行四边形ABCD中，DE、BF分别是∠ADC和∠ABC的角平分线，交AB、CD于点E、F，连接BD、EF．
（1）求证：BD、EF互相平分；
（2）若∠A=60°，AE=2EB，AD=4，求线段BD的长．
组卷：3438引用：11难度：0.4
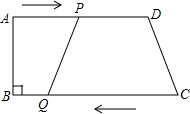23．如图，在梯形ABCD中，AD∥BC，∠B=90°，AB=10cm,AD=20cm,BC=24cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动，动点Q从点C开始沿CB方向向点B以3cm/s的速度运动．P、Q两点同时出发，设运动时间为t,当其中一点到达端点时，另一点随之停止运动．
（1）当t=3时，PD=
，CQ=
．
（2）当t为何值时，四边形CDPQ是平行四边形？请说明理由．
（3）在运动过程中，设四边形CDPQ的面积为S，写出S与t的函数关系式，并求当t为何值时，S的值最大，最大值是多少？
组卷：149引用：2难度：0.3
24．图1、图2均是3×4的正方形网格，每个小正方形的顶点称为格点．线段AB的端点均在格点上．在图1、图2给定网格中各画一个△APC，使点P在线段AB上，点C为格点．
要求：（1）图1中∠ACP的正切值为
1
2
，图2中∠ACP的正切值为
2
3
；
（2）只用无刻度的直尺，保留适当的作图痕迹．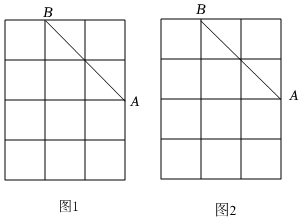
组卷：21引用：1难度：0.5
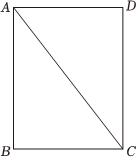
25．我国古代著作《九章算术》中记载了这样一个问题：“今有户不知高、广，竿不知长短．横之不出四尺，从之不出二尺，邪之适出．问户高、广、邪各几何？”其大意是：“今有门，不知其高、宽，有竿，不知其长短．横放，竿比门宽长出4尺；竖放，竿比门高长出2尺；斜放，竿与门对角线恰好相等．问门高、宽和对角线的长各是多少？”
问题：小明根据题意画出矩形ABCD，连接AC，请你结合小明所画的图求门高AB，门宽BC各是多少尺？
组卷：172引用：1难度：0.5
26．计算：
（1）
8
+
|
2
-
1
|
-
π
0
+
（
1
2
）
-
1
；
（2）
（
3
-
2
）
2021
•
（
3
+
2
）
2022
．
组卷：30引用：2难度：0.7