2020-2021学年新疆喀什地区疏勒县职业高中高三(上)第一次月考数学试卷
发布:2025/11/2 10:0:39
一、单选题
-
1.为了得到函数
,x∈R的图像,只需把函数y=sin2x,x∈R的图像( )y=sin(2x-π3)组卷:10引用:4难度:0.8 -
2.函数y=sin(x-
)是由y=sinx经过怎样的变化的得到的( )π4组卷:5引用:1难度:0.8 -
3.根据( )所给的条件,不能确定f(x)在x0处一定连续。
组卷:2引用:1难度:0.7 -
4.tan210°=( )
组卷:6引用:2难度:0.8 -
5.已知f(x)是奇函数,若方程f(x)=0有2021个实数根,则这2021个实数根之和为( )
组卷:1引用:1难度:0.9 -
6.已知
,则cos(60°-α)的值为( )sin(30°+α)=32组卷:40引用:1难度:0.5 -
7.在△ABC中,若a2=b2+bc+c2,则∠A为( )
组卷:30引用:7难度:0.9 -
8.在△ABC中,若A=60°,b=1,△ABC的面积
,则S=3=( )asinA组卷:23引用:2难度:0.8 -
9.在△ABC中,a、b、c分别为内角A、B、C所对的边,若a=8,B=60°,C=75°,则b=( )
组卷:1引用:2难度:0.7 -
10.函数y=sin2x,x∈R的最小正周期是( )
组卷:4引用:6难度:0.9 -
11.为了得到函数
的图象,需要把函数y=sin2x的图象( )y=sin(2x+π3)组卷:9引用:2难度:0.8 -
12.为得到函数
的图像,只需将函数y=sin2x的图像( )y=sin(2x+π3)组卷:28引用:2难度:0.8 -
13.cos222.5°-sin222.5°的值为( )
组卷:21引用:2难度:0.9 -
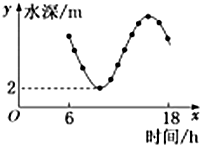 14.如图,某港口一天6时到18时的水深变化曲线近似满足函数,据此可知,这段时间水深(单位:m)的最大值为( )y=3sin(π6x+φ)+k组卷:9引用:1难度:0.8
14.如图,某港口一天6时到18时的水深变化曲线近似满足函数,据此可知,这段时间水深(单位:m)的最大值为( )y=3sin(π6x+φ)+k组卷:9引用:1难度:0.8 -
15.函数
的最小正周期为( )f(x)=4sin(6x+5π6)组卷:72引用:3难度:0.9 -
16.1-2sin215°的值为( )
组卷:115引用:3难度:0.8 -
17.若
,则cos2α等于( )sin(π2-α)=33组卷:25引用:1难度:0.5 -
18.已知△ABC的内角A,B,C的对边分别为a,b,c,且a2=b2-c2+
ac,则角B的大小是( )2组卷:14引用:2难度:0.9
二、填空题
-
19.函数
的单调递减区间是y=-2sinx.组卷:51引用:1难度:0.5 -
20.在△ABC中,角A,B,C所对的边长分别为a,b,c,若∠B=30°,a=6,
,则∠C=b=23.组卷:3引用:1难度:0.8 -
21.已知cosα=
,则cos2α=34.组卷:1引用:1难度:0.8 -
22.已知
,则cosα=cos2α=13,α∈(0,π2).组卷:28引用:1难度:0.9 -
23.已知函数f(x)=sinωx-cosωx,定义域为R,则函数f(x)的最大值是
.组卷:9引用:1难度:0.9 -
24.已知△ABC的内角A,B,C的对边分别为a,b,c,若a2=b2+2bcsinA,0<A<
,则tanA-4tanB的最小值为π2.组卷:0引用:1难度:0.5 -
25.已知在平面直角坐标系xOy中,角α的顶点在原点,始边与x轴的正半轴重合,终边经过点(2,4),则cos2α=
.组卷:12引用:1难度:0.5 -
26.已知△ABC中,角A、B、C所对的边分别为a、b、c,若
,则△ABC的面积为a=4+22-c,tanA=-7,cosC=34.组卷:3引用:1难度:0.8
三、解答题
-
27.已知角α的终边过点P(3,-4),求sinα,cosα,tanα.
组卷:21引用:7难度:0.8 -
28.用“五点法”画余弦函数y=cosx在
内的大致图象.x∈[-π2,3π2]组卷:22引用:1难度:0.9 -
29.在锐角△ABC中,角A,B,C所对的边分别为a,b,c,已知f(x)=
sinx+cosx,f(A)=3。3
(1)若b=2,c=3,求△ABC的面积S△ABC;
(2)若c2-b2=44,c=2b,求边长a的值。3组卷:14引用:2难度:0.6 -
 30.一艘海轮从A出发,沿北偏东75°的方向航行到达海岛B,然后从B出发,沿北偏东15°的方向航行4mile到达海岛C.(23-2)mile
30.一艘海轮从A出发,沿北偏东75°的方向航行到达海岛B,然后从B出发,沿北偏东15°的方向航行4mile到达海岛C.(23-2)mile
(1)求AC的长;
(2)如果下次航行直接从A出发到达C,求∠CAB的大小.组卷:14引用:1难度:0.6 -
31.
能否成立?如果能成立,那么cos(π3+4π3)=cosπ3是不是y=cosx的周期?为什么?4π3组卷:13引用:1难度:0.9


