当前位置：试卷中心 > 试卷详情

2020-2021学年新疆喀什地区疏勒县职业高中高三（上）第二次月考数学试卷

发布：2025/10/29 21:0:51

一、单选题

1．双曲线
x
2
9
-
y
2
4
=
1
的渐近线方程为（　　）
A．y=2x B．y=±
3
2
x
C．y=±
4
9
x
D．y=±
2
3
x
组卷：35引用：2难度：0.9
2．直线过抛物线x²=4y的焦点，且平分圆（x-1）²+y²=1，则该直线的方程为（　　）
A．y=x+1 B．y=-x+1 C．y=1 D．x=0
组卷：10引用：1难度：0.8
3．若抛物线y²=2px（p＞0）上一点M（2，y₀）到其准线的距离为4，则p等于（　　）
A．2 B．3 C．4 D．5
组卷：13引用：1难度：0.9
4．一动圆圆心在抛物线x²=4y上，动圆过抛物线的焦点F，并且恒与直线l相切，则直线l的方程为（　　）
A．x=1 B．y=-1 C．x=
1
16
D．y=-
1
16
组卷：3引用：1难度：0.9
5．椭圆
x
2
9
+
y
2
7
=
1
的焦点为F₁、F₂，点P在椭圆上，若|PF₂|=2，则|PF₁|=（　　）
A．1 B．2 C．3 D．4
组卷：17引用：1难度：0.9
6．已知双曲线
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的实轴长为2，且a²，b²，c²成等差数列，则双曲线的标准方程为（　　）
A．
x
2
2
-
y
2
=
1
B．
x
2
-
y
2
2
=
1
C．
x
2
4
-
y
2
8
=
1
D．
x
2
8
-
y
2
4
=
1
组卷：19引用：1难度：0.7
7．已知抛物线y²=2px的焦点与双曲线
x
2
3
-
y
2
6
=1的右焦点重合，则p的值（　　）
A．2 B．3 C．6 D．2
3
组卷：14引用：3难度：0.8
8．双曲线
x
2
20
-
y
2
5
=
1
的焦距为（　　）
A．
15
B．
2
15
C．5 D．10
组卷：104引用：2难度：0.8
9．椭圆短轴长为8，焦点为F₁（0，-3），F₂（0，3），则它的标准方程为（　　）
A．
x
2
91
+
y
2
100
=
1
B．
x
2
100
+
y
2
91
=
1
C．
x
2
25
+
y
2
16
=
1
D．
x
2
16
+
y
2
25
=
1
组卷：18引用：2难度：0.9
10．双曲线x²-y²=1的离心率是（　　）
A．
2
2
B．
3
C．
2
D．
1
2
组卷：54引用：2难度：0.9
11．已知一动点P到F₁（0，5），F₂（0，-5）的距离的差的绝对值为8，则动点P的轨迹方程为（　　）
A．
x
2
16
-
y
2
9
=
1
B．
x
2
3
-
y
2
4
=
1
C．
x
2
4
-
y
2
3
=
1
D．
y
2
16
-
x
2
9
=
1
组卷：6引用：1难度：0.7
12．一动圆圆心在抛物线x²=4y上，动圆过抛物线的焦点F，并且恒与直线l相切，则直线l的方程为（　　）
A．x=1 B．y=-1 C．x=
1
16
D．y=-
1
16
组卷：16引用：3难度：0.9
13．双曲线
x
2
3
-
y
2
4
=
1
的焦点坐标是（　　）
A．（0，±1） B．（±1，0） C．
（
0
，
±
7
）
D．
（
±
7
，
0
）
组卷：27引用：2难度：0.8
14．椭圆
x
2
25
+
y
2
16
=
1
的离心率为（　　）
A．
5
4
B．
3
4
C．
4
5
D．
3
5
组卷：114引用：5难度：0.8
15．焦点在x轴上，实轴长为8，虚轴长为2的双曲线的标准方程为（　　）
A．
y
2
16
-
x
2
=1 B．
y
2
64
-
x
2
4
=1 C．
x
2
16
-
y
2
=1 D．
x
2
64
-
y
2
4
=1
组卷：22引用：1难度：0.8
16．离心率为2的双曲线
x
2
a
2
-
y
2
b
2
=
1
的渐近线方程是（　　）
A．
5
x
±
y
=
0
B．x±y=0 C．
x
±
3
y
=
0
D．
3
x
±
y
=
0
组卷：10引用：2难度：0.8
17．点A在抛物线y²=-8x上且为第三象限的点，它到准线的距离为4，则点A到x轴的距离（　　）
A．2
2
B．2 C．4 D．2
3
组卷：42引用：2难度：0.7

二、填空题

18．已知椭圆
x
2
m
+
3
+
y
2
4
=
1
的离心率
e
=
1
3
，则 m的值等于

．
组卷：22引用：1难度：0.7
19．已知椭圆中心在原点，一个焦点为F（-2
3
，0），且长轴长是短轴长的2倍，则该椭圆的标准方程是

．
组卷：7引用：1难度：0.7
20．已知点P（1，1）在抛物线C：y²=2px（p＞0）上，F是抛物线C的焦点，则|PF|的值为

．
组卷：11引用：1难度：0.8
21．双曲线
x
2
9
-
y
2
16
=
1
的离心率为

；渐近线为

．
组卷：13引用：1难度：0.7
22．已知点
A
（
1
，
2
）
在抛物线C：y²=2px上，F为C的焦点，则|AF|=

．
组卷：52引用：4难度：0.8
23．已知椭圆
x
2
4
+
y
2
2
=
1
的两个焦点是F₁、F₂，点P在椭圆上，若|PF₂|-|PF₁|=2，则ΔPF₁F₂的面积是

.
组卷：10引用：1难度：0.9
24．若某曲线上任意一点P到点（3，0）的距离与到直线x=-3的距离相等，则该曲线方程为

．
组卷：18引用：1难度：0.8
25．系统找不到该试题

三、解答题

26．已知抛物线y=2x²-4x+c与x轴有两个不同的交点．
（1）求c的取值范围；
（2）求抛物线y=2x²-4x+c的对称轴，若抛物线经过点A（2，m）和点B（3，n），试比较m和n的大小，并说明理由．
组卷：4引用：1难度：0.6
27．求两条渐近线为x±2y=0且截直线x-y-3=0所得弦长为
8
3
3
的双曲线方程。
组卷：6引用：1难度：0.6
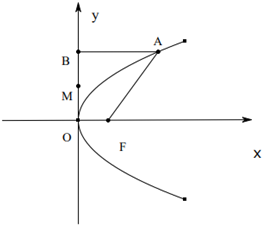28．如图，已知抛物线y²=2px（p＞0）的焦点为F，A是抛物线上横坐标为4，且位于x轴上方的点，A到抛物线准线的距离等于5，过A作AB垂直于y轴，垂足为B，OB的中点为M．
（1）求抛物线的方程；
（2）以AF为直径作圆C，请判断点M与圆C的位置关系，并说明理由．
组卷：3引用：1难度：0.6
29．已知椭圆
x
2
4
+
y
2
m
=
1
与抛物线y²=4x有共同的焦点F₂，过椭圆的左焦点F₁作倾角为
π
4
的直线，与椭圆交于M，N两点，求：
（1）直线MN的方程和椭圆的方程；
（2）△OMN的面积．
组卷：29引用：2难度：0.5
30．如图，曲线C₁是以原点O为中心，F₁、F₂为焦点的椭圆的一部分，曲线C₂是以原点O为顶点，F₂为焦点的抛物线的一部分，
A
（
3
2
，
6
）
是曲线C₁和C₂的交点．
（Ⅰ）求曲线C₁和C₂所在的椭圆和抛物线的方程；
（Ⅱ）过F₂作一条与x轴不垂直的直线，分别与曲线C₁、C₂依次交于B、C、D、E四点，若G为CD中点，H为BE中点，问
|
BE
|
•
|
G
F
2
|
|
CD
|
•
|
H
F
2
|
是否为定值，若是，求出定值；若不是，请说明理由．
组卷：161引用：2难度：0.3

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A． x 2 91 + y 2 100 = 1	B． x 2 100 + y 2 91 = 1
C． x 2 25 + y 2 16 = 1	D． x 2 16 + y 2 25 = 1

2020-2021学年新疆喀什地区疏勒县职业高中高三（上）第二次月考数学试卷

一、单选题

1．双曲线x29-y24=1的渐近线方程为（ ）

2．直线过抛物线x2=4y的焦点，且平分圆（x-1）2+y2=1，则该直线的方程为（ ）

3．若抛物线y2=2px（p＞0）上一点M（2，y0）到其准线的距离为4，则p等于（ ）

4．一动圆圆心在抛物线x2=4y上，动圆过抛物线的焦点F，并且恒与直线l相切，则直线l的方程为（ ）

5．椭圆x29+y27=1的焦点为F1、F2，点P在椭圆上，若|PF2|=2，则|PF1|=（ ）

6．已知双曲线x2a2-y2b2=1（a＞0，b＞0）的实轴长为2，且a2，b2，c2成等差数列，则双曲线的标准方程为（ ）

7．已知抛物线y2=2px的焦点与双曲线x23-y26=1的右焦点重合，则p的值（ ）

8．双曲线x220-y25=1的焦距为（ ）

9．椭圆短轴长为8，焦点为F1（0，-3），F2（0，3），则它的标准方程为（ ）

10．双曲线x2-y2=1的离心率是（ ）

11．已知一动点P到F1（0，5），F2（0，-5）的距离的差的绝对值为8，则动点P的轨迹方程为（ ）

12．一动圆圆心在抛物线x2=4y上，动圆过抛物线的焦点F，并且恒与直线l相切，则直线l的方程为（ ）

13．双曲线x23-y24=1的焦点坐标是（ ）

14．椭圆x225+y216=1的离心率为（ ）

15．焦点在x轴上，实轴长为8，虚轴长为2的双曲线的标准方程为（ ）

16．离心率为2的双曲线x2a2-y2b2=1的渐近线方程是（ ）

17．点A在抛物线y2=-8x上且为第三象限的点，它到准线的距离为4，则点A到x轴的距离（ ）

二、填空题

18．已知椭圆 x2m+3+y24=1的离心率 e=13，则 m的值等于 ．

19．已知椭圆中心在原点，一个焦点为F（-23，0），且长轴长是短轴长的2倍，则该椭圆的标准方程是 ．

20．已知点P（1，1）在抛物线C：y2=2px（p＞0）上，F是抛物线C的焦点，则|PF|的值为 ．

21．双曲线x29-y216=1的离心率为 ；渐近线为 ．

22．已知点A（1，2）在抛物线C：y2=2px上，F为C的焦点，则|AF|= ．

23．已知椭圆x24+y22=1的两个焦点是F1、F2，点P在椭圆上，若|PF2|-|PF1|=2，则ΔPF1F2的面积是 .

24．若某曲线上任意一点P到点（3，0）的距离与到直线x=-3的距离相等，则该曲线方程为 ．

三、解答题

26．已知抛物线y=2x2-4x+c与x轴有两个不同的交点．（1）求c的取值范围；（2）求抛物线y=2x2-4x+c的对称轴，若抛物线经过点A（2，m）和点B（3，n），试比较m和n的大小，并说明理由．

27．求两条渐近线为x±2y=0且截直线x-y-3=0所得弦长为833的双曲线方程。

29．已知椭圆x24+y2m=1与抛物线y2=4x有共同的焦点F2，过椭圆的左焦点F1作倾角为π4的直线，与椭圆交于M，N两点，求：（1）直线MN的方程和椭圆的方程；（2）△OMN的面积．

1．双曲线
x
2
9
-
y
2
4
=
1
的渐近线方程为（　　）

2．直线过抛物线x²=4y的焦点，且平分圆（x-1）²+y²=1，则该直线的方程为（　　）

3．若抛物线y²=2px（p＞0）上一点M（2，y₀）到其准线的距离为4，则p等于（　　）

4．一动圆圆心在抛物线x²=4y上，动圆过抛物线的焦点F，并且恒与直线l相切，则直线l的方程为（　　）

5．椭圆
x
2
9
+
y
2
7
=
1
的焦点为F₁、F₂，点P在椭圆上，若|PF₂|=2，则|PF₁|=（　　）

6．已知双曲线
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的实轴长为2，且a²，b²，c²成等差数列，则双曲线的标准方程为（　　）

7．已知抛物线y²=2px的焦点与双曲线
x
2
3
-
y
2
6
=1的右焦点重合，则p的值（　　）

8．双曲线
x
2
20
-
y
2
5
=
1
的焦距为（　　）

9．椭圆短轴长为8，焦点为F₁（0，-3），F₂（0，3），则它的标准方程为（　　）

10．双曲线x²-y²=1的离心率是（　　）

11．已知一动点P到F₁（0，5），F₂（0，-5）的距离的差的绝对值为8，则动点P的轨迹方程为（　　）

12．一动圆圆心在抛物线x²=4y上，动圆过抛物线的焦点F，并且恒与直线l相切，则直线l的方程为（　　）

13．双曲线
x
2
3
-
y
2
4
=
1
的焦点坐标是（　　）

14．椭圆
x
2
25
+
y
2
16
=
1
的离心率为（　　）

15．焦点在x轴上，实轴长为8，虚轴长为2的双曲线的标准方程为（　　）

16．离心率为2的双曲线
x
2
a
2
-
y
2
b
2
=
1
的渐近线方程是（　　）

17．点A在抛物线y²=-8x上且为第三象限的点，它到准线的距离为4，则点A到x轴的距离（　　）

18．已知椭圆
x
2
m
+
3
+
y
2
4
=
1
的离心率
e
=
1
3
，则 m的值等于

．

19．已知椭圆中心在原点，一个焦点为F（-2
3
，0），且长轴长是短轴长的2倍，则该椭圆的标准方程是

．

20．已知点P（1，1）在抛物线C：y²=2px（p＞0）上，F是抛物线C的焦点，则|PF|的值为

．

21．双曲线
x
2
9
-
y
2
16
=
1
的离心率为

；渐近线为

．

22．已知点
A
（
1
，
2
）
在抛物线C：y²=2px上，F为C的焦点，则|AF|=

．

23．已知椭圆
x
2
4
+
y
2
2
=
1
的两个焦点是F₁、F₂，点P在椭圆上，若|PF₂|-|PF₁|=2，则ΔPF₁F₂的面积是

.

24．若某曲线上任意一点P到点（3，0）的距离与到直线x=-3的距离相等，则该曲线方程为

．

26．已知抛物线y=2x²-4x+c与x轴有两个不同的交点．
（1）求c的取值范围；
（2）求抛物线y=2x²-4x+c的对称轴，若抛物线经过点A（2，m）和点B（3，n），试比较m和n的大小，并说明理由．

27．求两条渐近线为x±2y=0且截直线x-y-3=0所得弦长为
8
3
3
的双曲线方程。

29．已知椭圆
x
2
4
+
y
2
m
=
1
与抛物线y²=4x有共同的焦点F₂，过椭圆的左焦点F₁作倾角为
π
4
的直线，与椭圆交于M，N两点，求：
（1）直线MN的方程和椭圆的方程；
（2）△OMN的面积．