2022-2023学年浙江省宁波市镇海区蛟川书院八年级（下）期中数学试卷

一、选择题（本题有10小题，每小题4分，共40分．请选出各题中唯一的正确选项，不

• 1．下列二次根式中，是最简二次根式的是（　　）

  A． 0 . 1

  B． 30

  C． 1 2

  D． 18
  组卷：468引用：5难度：0.8

  解析

• 2．中国航天取得了举世瞩目的成就，为人类和平贡献了中国智慧和中国力量，下列是有关中国航天的图标，其文字上方的图案是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：1179引用：57难度：0.8

  解析

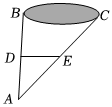• 3．如图，要测量B，C两地的距离，小明想出一个方法：在池塘外取点A，得到线段AB，AC，并取AB，AC的中点D，E，连结DE，则他只需测量（　　）

  A．AD长

  B．AE长

  C．DE长

  D．AC长
  组卷：318引用：6难度：0.7

  解析

• 4．在▱ABCD中，∠A+∠C=160°，则∠B的度数为（　　）

  A．60°

  B．80°

  C．100°

  D．120°
  组卷：112引用：5难度：0.8

  解析

• 5．2021年，党中央国务院赋予浙江省建设“共同富裕示范区”的光荣使命．共同富裕的要求是：在消除两极分化和贫穷基础上实现普遍富裕．下列有关人均收入的统计量特征中，最能体现共同富裕要求的是（　　）

  A．平均数大，方差大	B．平均数大，方差小
  C．平均数小，方差小	D．平均数小，方差大
  组卷：187引用：4难度：0.7

  解析

• 6．若点A（x₁，y₁）、B（x₂，y₂）、C（x₃，y₃）都在反比例函数

  y

  =

  -

  2

  x

  的图象上，且x₁＜0＜x₂＜x₃，则y₁、y₂、y₃的大小关系是（　　）

  A．y1＜y3＜y2

  B．y2＜y3＜y3

  C．y1＜y2＜y3

  D．y2＜y3＜y1
  组卷：141引用：3难度：0.9

  解析

• 7．用反证法证明“三角形中至少有两个角是锐角”时，首先应该假设这个三角形中（　　）

  A．每一个角是锐角

  B．每一个角都是钝角或直角

  C．至多有一个角是锐角

  D．至多有一个角是钝角或直角
  组卷：439引用：3难度：0.7

  解析

• 8．若关于x的一元二次方程ax²+bx+c=0有一个根是1，则下列说法不一定正确的是（　　）

  A．a≠0

  B．a+b+c=0

  C．a=c

  D．b2-4ac≥0
  组卷：471引用：4难度：0.7

  解析

三、解答题（本题有8小题，第17～19题每题8分，第20～22题每题10分，第23题12分，第24题14分，共80分）

• 23．【基础巩固】
  （1）如图1，P是矩形ABCD内部一点，求证：PA²+PC²=PB²+PD².请你将下面的证明过程补充完整．
  证明：过P分别作边AB，AD的平行线EF，GH交AD于E，交BC于F，交AB于G，交CD于H．设PE=a,PF=b,PG=c,PH=d.
  

  （请在框内证明：四边形AGPE是矩形）

  同理可证四边形DHPE，四边形BGPF，四边形CFPH均是矩形
  ∴PA²+PC²=PB²+PD²=

  （用关于a,b,c,d的代数式填空）
  【尝试应用】
  （2）如图2，P为正方形ABCD内一点，且PA：PB：PC=1：

  3

  ：

  5

  ，求∠PAB的大小．
  【拓展提高】
  （3）如图3，在Rt△ABC中，∠BAC=90°，点D，E是斜边BC上的三等分点．若AD=3，AE=4，求BC的长．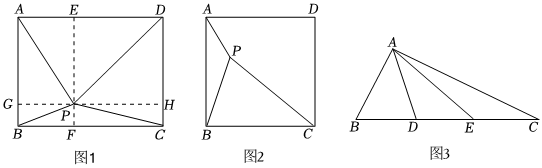
  
  组卷：331引用：1难度：0.1

  解析

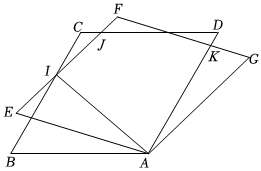• 24．如图，在菱形ABCD中，AB=3，∠B=60°．将菱形ABCD绕点A顺时针旋转，旋转角为α（0°＜α＜60°），得到菱形AEFG，EF与BC，CD分别交于点I，J，AE与BC交于点H，FG与AD交于点K，连接AI．
  （1）用含α的代数式表示∠BIE；
  （2）求证：AI平分∠BIF；
  （3）在α从0°到60°的变化过程中，
  ①△CIJ的周长是否变化？若不变，请求出△CIJ的周长；若变化，请说明理由．
  ②直接写出点K的运动路径长．
  组卷：238引用：1难度：0.1

  解析