2023年安徽省黄山市黟县美溪初级中学中考数学适应性试卷

一、选择题（本题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．-（-2023）=（　　）

  A．-2023

  B．2023

  C． - 1 2023

  D． 1 2023
  组卷：2093引用：20难度：0.9

  解析

• 2．下列运算正确的是（　　）

  A．a5÷a2=a3	B．3a2+a=3a3
  C．（a4）3=a7	D．a（a+1）=a2+1
  组卷：112引用：2难度：0.5

  解析

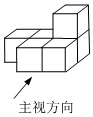• 3．如图所示的几何体是由6个大小相同的小正方体组成，它的主视图为（　　）

  A．

  B．

  C．

  D．
  组卷：161引用：7难度：0.8

  解析

• 4．下列标志中，只是中心对称图形，不是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：79引用：12难度：0.9

  解析

• 5．某中学随机地调查了50名学生，了解他们一周在校的体育锻炼时间，结果如下表所示：
  

  时间（小时）	5	6	7	8
  人数	10	15	20	5

  则这50名学生这一周在校的平均体育锻炼时间是（　　）

  A．6.2小时

  B．6.4小时

  C．6.5小时

  D．7小时
  组卷：880引用：79难度：0.9

  解析

• 6．一元二次方程2x²-3x-4=0的根的情况是（　　）

  A．有一个实数根	B．有两个不相等的实数根
  C．没有实数根	D．有两个相等的实数根
  组卷：221引用：5难度：0.8

  解析

• 7．某市为了方便市民绿色出行，推出了共享单车服务．图①是某品牌共享单车放在水平地面的实物图，图②是其示意图，其中AB，CD都与地面l平行，∠BCD=60°，∠BAC=54°．当∠MAC为（　　）度时，AM与CB平行．
  

  A．16

  B．60

  C．66

  D．114
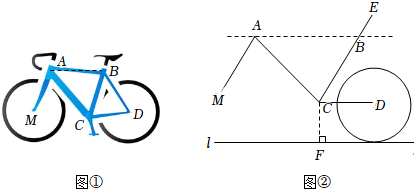  组卷：813引用：14难度：0.7

  解析

• 8．《九章算术》是人类科学史上应用数学的“算经之首”，书中记载：今有二人共车九人步；三人共车，二车空．问：人与车各几何？译文：若每辆车都坐2人，则9需要步行：若每辆车都坐3人，则两辆车是空的，问：车与人各多少？设有x辆车，y个人，根据题意，列方程组是（　　）

  A． y = 2 x + 9 y = 3 x - 2	B． y = 2 x + 9 y = 3 （ x - 2 ）
  C． y = 2 x - 9 y = 3 x - 2	D． y = 2 x - 9 y = 3 （ x - 2 ）
  组卷：288引用：9难度：0.7

  解析

七、解答题（满分12分）

• 25．已知△ABC和△ADE均为等腰直角三角形，△ADE绕点A逆时针旋转一周．
  
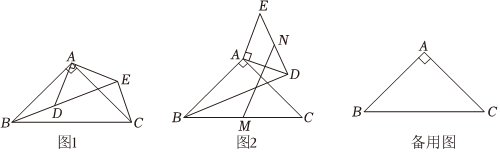
  （1）如图1，连接BD，CE，则BD与CE的数量关系为

  ；直线BD与CE所夹角的度数为

  ；
  （2）当△ADE旋转至如图2所示的位置时，取BC，DE的中点M，N，连接MN，BD．试问：

  MN

  BD

  的值是否随△ADE的旋转而变化？若不变，请求出该值；若变化，请说明理由；
  （3）M，N分别为BC，DE的中点，连接MN．若

  AB

  =

  3

  10

  ，AD=6，当△ADE旋转至B，D，E三点在同一条直线上时，请直接写出MN的值．
  组卷：139引用：2难度：0.3

  解析

八、解答题（满分14分）

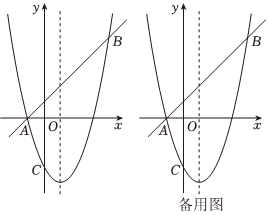• 26．如图，对称轴为直线x=1的抛物线经过A（-1，0），B（4，5）两点，与y轴交于点C．
  （1）求抛物线的解析式；
  （2）若P为直线AB上一点，连接PC，将PC绕点P顺时针旋转90°得到线段PD，当点D在抛物线上时，求点P的坐标；
  （3）已知点E在对称轴上，连接AE，BE，当△ABE为钝角三角形时，请直接写出点E的纵坐标n的取值范围．
  组卷：52引用：2难度：0.3

  解析