2022-2023学年福建省厦门外国语学校石狮分校八年级（上）期中数学试卷

一．选择题：（本题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．）

• 1．36的平方根是（　　）

  A．6

  B．-6

  C．4或9

  D．±6
  组卷：245引用：4难度：0.7

  解析

• 2．在下列实数中，无理数的是（　　）

  A．0.3

  B．0

  C． 7

  D． 25
  组卷：19引用：4难度：0.8

  解析

• 3．下列各组数据中，不能作为直角三角形三边长的是（　　）

  A．9，12，15

  B．3，4，5

  C．6，8，11

  D．7，24，25
  组卷：85引用：3难度：0.5

  解析

• 4．下列多项式中能用平方差公式分解因式的是（　　）

  A．x2+y2

  B．-a2-b2

  C．x3-y2

  D．a2-b2
  组卷：639引用：6难度：0.8

  解析

• 5．下列计算结果为x⁶的是（　　）

  A．x3•x2

  B．x3+x3

  C．（x4）2

  D．x7÷x
  组卷：227引用：5难度：0.9

  解析

• 6．如图，在Rt△ABC中，∠ACB=90°，分别以AC，BC，AB为边在三角形外部作正方形．若以AC和BC为边的正方形面积分别为5和3，则以AB为边的正方形面积S的值为（　　）

  A．4

  B．8

  C． 2 2

  D．34
  组卷：288引用：4难度：0.6

  解析

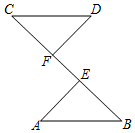• 7．如图，BF=CE，AE⊥BC，DF⊥BC，添加一个条件____，即可证明Rt△ABE≌Rt△DCF．下列添加的条件不正确的是（　　）

  A．AB=DC

  B．AE=BF

  C．EA=FD

  D．∠A=∠D
  组卷：520引用：6难度：0.6

  解析

• 8．如图，A、B、C表示三个居民小区，为了居民生活的方便，现准备建一个生活超市，使它到这三个居民小区的距离相等，那么生活超市应建在（　　）

  A．AB，AC两边中线的交点处

  B．AB，AC两边高线的交点处

  C．∠B与∠C这两个角的角平分线的交点处

  D．AB，AC两边的垂直平分线的交点处
  组卷：479引用：8难度：0.8

  解析

三、解答题（本题有9个小题，共86分.解答应写出文字说明、证明过程或演算步骤）

• 24．已知△ABC≌△ADE，且它们都是等腰直角三角形，∠ABC=∠ADE=90°．
  （1）如图1，当点D在边AC上时，连接BD并延长交CE于点F，
  ①求证：∠CBD=∠EDF；
  ②求证：点F为线段CE的中点；
  （2）△ADE绕着点A顺时针旋转，如图2所示，连接BD并延长交CE于点F，点F还是线段CE的中点吗？请说明理由．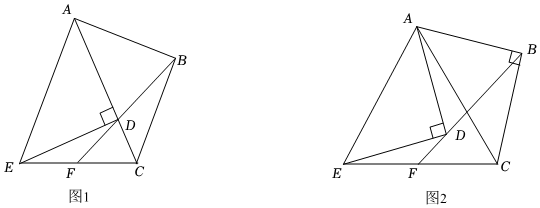
  
  组卷：215引用：3难度：0.4

  解析

• 25．如图，正方形ABCD的边长为a,射线AM是∠BAD外角的平分线，点E在边AB上运动（不与点A、B重合），点F在射线AM上，且

  AF

  =

  2

  BE

  ，CF与AD相交于点G，连接EC、EF、EG．
  
  （1）试猜想△CEF的形状，并说明理由；
  （2）求△AEG的周长（用含a的代数式表示）；
  （3）试探索：点E在边AB上运动至什么位置时，△EAF的面积最大（用含a的代数式表示）．
  组卷：26引用：2难度：0.1

  解析