2021-2022学年辽宁省大连三十七中九年级（上）第一次月考数学试卷

一、选择题（本题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一个选项正确）

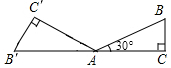• 1．如图所示，将一个含30°角的直角三角板ABC绕点A逆时针旋转，点B的对应点是点B′，若点B′、A、C在同一条直线上，则三角板ABC旋转的度数是（　　）

  A．60°

  B．90°

  C．120°

  D．150°
  组卷：1187引用：13难度：0.7

  解析

• 2．在Rt△ABC中，∠C=90°，若AC=2BC，则tanA的值是（　　）

  A． 1 2

  B．2

  C． 5 5

  D． 5 2
  组卷：66引用：2难度：0.5

  解析

• 3．如图，某书店拿取高处书籍的登高梯AC靠书架放置，顶端A恰好放在书架第七层的顶端，已知AC=3米，∠CAB=18°，则书架第七层顶端离地面的高度AB为（　　）

  A． 3 sin 18 ° 米

  B．3sin18°米

  C． 3 cos 18 ° 米

  D．3cos18°米
  组卷：78引用：3难度：0.7

  解析

• 4．如图，等边△ABC的边长为6，P为BC上一点，BP=2，D为AC上一点，若∠APD=60°，则CD的长为（　　）

  A．2

  B． 4 3

  C． 2 3

  D．1
  组卷：767引用：6难度：0.7

  解析

• 5．如图，在▱ABCD中，EF∥AB，DE：EA=2：3，EF=4，则CD的长为（　　）

  A． 16 3

  B．8

  C．10

  D．16
  组卷：1491引用：33难度：0.9

  解析

• 6．下列四个图形中，既是轴对称图形，又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：1489引用：28难度：0.7

  解析

• 7．一个五边形的边长分别为2、3、4、5、6，另一个和它相似的五边形的最大边长为24，则这个五边形的最短边为（　　）

  A．6

  B．8

  C．10

  D．12
  组卷：175引用：5难度：0.9

  解析

• 8．在直角三角形ABC中，∠BAC=90°，AD⊥BC，AB=4，CD=6，那么正确的（　　）

  A．∠C=60°

  B．AD=2 3

  C．AC2=BD×CD

  D．AC=4 2
  组卷：394引用：3难度：0.7

  解析

• 9．如图，小明晚上由路灯A下的点B处走到点C处时，测得自身影子CD的长为1米，他继续往前走3米到达点E处（即CE=3米），测得自己影子EF的长为2米，已知小明的身高是1.5米，那么路灯A的高度AB是（　　）

  A．4.5米

  B．6米

  C．7.2米

  D．8米
  组卷：1786引用：14难度：0.7

  解析

• 10．在平面直角坐标系xOy中，点P（2，-3）关于原点O对称的点的坐标是（　　）

  A．（2，3）

  B．（-2，3）

  C．（-2，-3）

  D．（2，-3）
  组卷：137引用：3难度：0.9

  解析

二、填空题（本题共6小题，每小题3分，共18分）

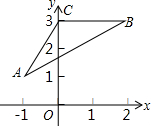• 11．如图，在直角坐标系中，△ABC的各顶点坐标为A（-1，1），B（2，3），C（0，3）．现以坐标原点为位似中心，作△A′B′C′，使△A′B′C′与△ABC的位似比为

  2

  3

  ．则点A的对应点A′的坐标为

   

  ．
  组卷：906引用：6难度：0.7

  解析

• 12．如图，在矩形ABCD中，连接BD，点E在AD上，连接CE，交BD于点F，且△DEF∽△DBA．
  （1）BD与CE是否垂直？

  （填“是”或“否”）；
  （2）若AB=1，∠CBD=30°，则

  EF

  CF

  的值为

  ．
  组卷：186引用：4难度：0.7

  解析

• 13．东东和爸爸到广场散步，爸爸的身高是176cm,东东的身高是156cm,在同一时刻爸爸的影长是88cm,那么东东的影长是

  cm.
  组卷：110引用：37难度：0.7

  解析

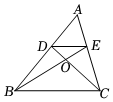• 14．如图，D、E分别是△ABC的边AB、AC上的点，且DE∥BC，BE、CD相交于点O，若S_△DOE：S_△DOB=1：3，则

  DE

  BC

  =

  ，当S_△ADE=2时，四边形DBCE的面积是

  ．
  组卷：634引用：3难度：0.6

  解析

• 15．已知

  x

  y

  =

  5

  2

  ，则

  x

  -

  y

  y

  的值是

  ．
  组卷：733引用：20难度：0.7

  解析

• 16．计算：tan45°+sin²60°=

  ．
  组卷：32引用：1难度：0.8

  解析

三、解答题（本题共4小题，其中17，18，19题各9分，20题12分，共39分）

• 17．计算：

  tan

  45

  °

  3

  tan

  30

  °

  -

  2

  sin

  45

  °

  -

  co

  s

  2

  30

  °

  cot

  30

  °

  ．
  组卷：671引用：3难度：0.5

  解析

• 18．如图1，点O在线段AB上，AO=2，OB=1，OC为射线，且∠BOC=60°，动点P以每秒2个单位长度的速度从点O出发，沿射线OC做匀速运动，设运动时间为t秒．
  （1）当t=

  1

  2

  秒时，则OP=

   

  ，S_△ABP=

   

  ；
  （2）当△ABP是直角三角形时，求t的值；
  （3）如图2，当AP=AB时，过点A作AQ∥BP，并使得∠QOP=∠B，求证：AQ•BP=3．
  
  组卷：2259引用：8难度：0.1

  解析

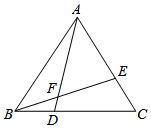• 19．如图，△ABC是等边三角形，点D，E分别在BC，AC上，且BD=CE，AD与BE相交于点F，
  （Ⅰ）证明：△ABD≌△BCE；
  （Ⅱ）证明：△ABE∽△FAE；
  （Ⅲ）若AF=7，DF=1，求BD的长．
  组卷：6418引用：6难度：0.5

  解析

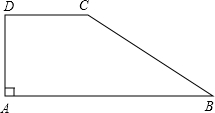• 20．如图，在梯形ABCD中，AB∥CD，∠A=90°，CD=4，AB=10，

  tan

  ∠

  B

  =

  2

  3

  ．求BC的长．
  组卷：31引用：2难度：0.5

  解析

四、解答题（本题共3小题，其中21题9分，22、23题各10分，共29分）

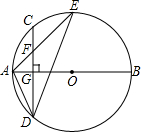• 21．如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足

  CF

  FD

  =

  1

  3

  ，连接AF并延长交⊙O于点E，连接AD、DE，若CF=2，AF=3．
  （1）求证：△ADF∽△AED；
  （2）求FG的长；
  （3）求证：tan∠E=

  5

  4

  ．
  组卷：2322引用：60难度：0.1

  解析

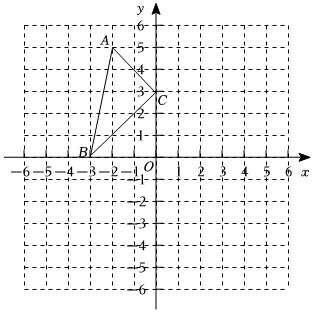• 22．在下列的网格图中按照要求画出图形，并回答问题．
  （1）以O为位似中心，在第四象限内将△ABC缩小为原来的

  1

  2

  得到△A'B'C'；
  （2）写出△A'B'C'各顶点的坐标及△A'B'C'的面积．
  组卷：2引用：0难度：0.5

  解析

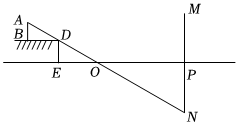• 23．如图，为了测量平静的河面的宽度（EP），在离河岸D点3m远的B点，立一根长为1.5m的标杆AB，已知河岸高出水面0.6m,即DE=0.6m.在河对岸的水里有一棵高出水面4.6m的大树MP，大树的顶端M在河里的倒影为点N，即PM=PN．经测量此时A，D，N三点在同一直线上，并且点M，P，N共线，若AB，DE，MP均垂直于河面EP，则河宽EP是多少米？
  ​
  组卷：319引用：2难度：0.4

  解析

五、解答题（本题共3小题，其中24、25题各11分，26题12分，共34分）

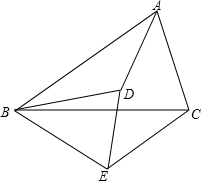• 24．已知，如图，

  AB

  BD

  =

  BC

  BE

  =

  CA

  ED

  ，那么△ABD与△BCE相似吗？为什么？
  组卷：2008引用：3难度：0.7

  解析

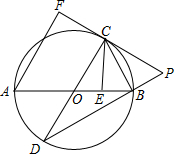• 25．如图，AB是⊙O的直径，AB=4

  3

  ，点E为线段OB上一点（不与O，B重合），作CE⊥OB，交⊙O于点C，垂足为点E，作直径CD，过点C的切线交DB的延长线于点P，AF⊥PC于点F，连接CB．
  （1）求证：CB是∠ECP的平分线；
  （2）求证：CF=CE；
  （3）当

  CF

  CP

  =

  3

  4

  时，求劣弧

  ˆ

  BC

  的长度（结果保留π）
  组卷：5805引用：6难度：0.3

  解析

• 26．已知Rt△ABC，∠ACB=90°，D为AB边上一点（不与A、B重合），以CD为底作等腰△CDE，使A、E位于CD两侧，且∠DCE=∠A．
  （1）如图1，若∠B=25°，求∠E的度数；
  （2）如图2，若CA=CD，BC=2AC，DE交BC于F点，求

  EF

  DF

  的值；
  （3）如图1，连接BE，求证：DE=BE．
  
  组卷：146引用：2难度：0.1

  解析