2022-2023学年北京市石景山区八年级（下）期中数学试卷

一.选择题

• 1．若3a=4b（ab≠0），则下列比例式成立的是（　　）

  A． a 4 = b 3

  B． a 3 = b 4

  C． a b = 3 4

  D． a 4 = 3 b
  组卷：705引用：7难度：0.9

  解析

• 2．抛物线y=x²-1的顶点坐标（　　）

  A．（0，1）

  B．（1，0）

  C．（0，-1）

  D．（-1，0）
  组卷：862引用：1难度：0.7

  解析

• 3．将抛物线y=x²向左平移3个单位长度，再向上平移2个单位长度，得到抛物线的表达式为（　　）

  A．y=（x+3）2-2

  B．y=（x+3）2+2

  C．y=（x-3）2+2

  D．y=（x-3）2-2
  组卷：246引用：1难度：0.5

  解析

• 4．如图，五线谱由五条等距离的平行横线组成，同一条直线上的三个点A，B，C都在横线上，若线段AB=6，则线段BC的长是（　　）
  ​

  A．4

  B．3

  C．2

  D．1
  组卷：321引用：5难度：0.7

  解析

• 5．已知抛物线y=2x²+8x-6，下列说法正确的是（　　）

  A．抛物线的开口方向向下

  B．抛物线的对称轴是直线x=2

  C．抛物线与y轴交于点（0，-6）

  D．抛物线与x轴没有交点
  组卷：780引用：5难度：0.8

  解析

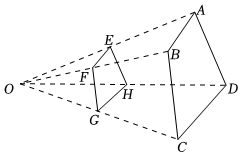• 6．如图，四边形ABCD与四边形EFGH是位似图形，点O是位似中心．若

  OE

  EA

  =

  2

  3

  ，四边形ABCD的面积是100，则四边形EFGH的面积是（　　）

  A．4

  B．16

  C．36

  D． 100 9
  组卷：482引用：3难度：0.5

  解析

• 7．2022年北京冬奥会举办期间，冬奥会吉祥物“冰墩墩”深受广大人民的喜爱．某特许零售店“冰墩墩”的销售日益火爆，每个纪念品进价40元．销售期间发现，当销售单价定为44元时，每天可售出300个，销售单价每降价1元，每天销量增加20个．现商家决定降价销售，设每天销售量为y个，销售单价为x元（40＜x＜44），商家每天销售纪念品获得的利润w元，则下列等式正确的是（　　）

  A．y=20x-580	B．y=-20x+300
  C．w=（20x-480）（x-40）	D．w=（-20x+1180）（x-40）
  组卷：951引用：4难度：0.7

  解析

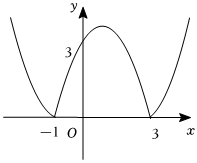• 8．我们定义一种新函数：形如y=|ax²+bx+c|（a≠0，b²-4ac＞0）的函数叫做“鹊桥”函数．数学兴趣小组画出一个“鹊桥”函数y=|x²+bx+c|的图象如图所示，则下列结论正确的是（　　）

  A．bc＜0

  B．c=3

  C．当直线y=x+m与该图象恰有三个公共点时，则m=1

  D．关于x的方程|x2+bx+c|=3的所有实数根的和为4
  组卷：2422引用：22难度：0.6

  解析

二．填空题

• 9．已知函数y=（m+1）x^|m|+1-2x+1是二次函数，则m=

  ．
  组卷：1320引用：7难度：0.8

  解析

三．解答题

• 27．如图1，点C将线段AB分成两部分，如果

  AC

  AB

  =

  BC

  AC

  ，那么称点C为线段AB的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为s的图形分成两部分，这两部分的面积分别为S₁，S₂，如果

  s

  1

  s

  =

  s

  2

  s

  1

  ，那么称直线l为该图形的黄金分割线．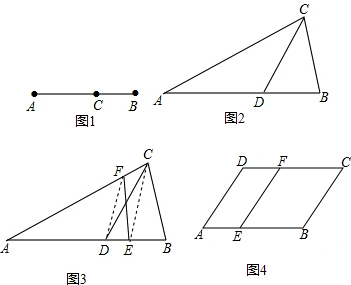
  
  （1）研究小组猜想：在三角形ABC中，若点D为AB边上的黄金分割点（如图2），则直线CD是三角形ABC的黄金分割线．你认为对吗？为什么？
  （2）请你说明：三角形的中线是否也是该三角形ABC的黄金分割线？
  （3）研究小组在进一步探究中发现：过点C任作一条直线交AB于点E，再过点D（D为AB边上的黄金分割点）作直线DF，且DF∥CE，交AC于点F，连接EF（如图3），则直线EF也是三角形ABC的黄金分割线．
  请你说明理由．
  （4）如图4，点E是平行四边形ABCD的边AB的黄金分割点，过点E作EF平行AD，交DC于点F，显然直线EF是平行四边形ABCD的黄金分割线．请你画一条平行四边形ABCD的黄金分割线，使它不经过平行四边形ABCD各边黄金分割点．
  组卷：333引用：4难度：0.3

  解析

• 28．定义：函数图象上到两坐标轴的距离都不大于n（n≥0）的点叫做这个函数图象的“n阶方点”．例如，点（

  1

  3

  ，

  1

  3

  ）是函数y=x图象的“

  1

  2

  阶方点”；点（2，1）是函数y=

  2

  x

  图象的“2阶方点”．
  （1）在①（-2，-

  1

  2

  ）；②（-1，-1）；③（1，1）三点中，是反比例函数y=

  1

  x

  图象的“1阶方点”的有

  （填序号）；
  （2）若y关于x的一次函数y=ax-3a+1图象的“2阶方点”有且只有一个，求a的值；
  （3）若y关于x的二次函数y=-（x-n）²-2n+1图象的“n阶方点”一定存在，请直接写出n的取值范围．
  组卷：3410引用：7难度：0.3

  解析