2022-2023学年江苏省淮安市盱眙县七年级(下)期中数学试卷
发布:2024/7/4 8:0:9
一、选择题(本题共8小题,每小题3分,共24分.每题的四个选项中,只有一个符合题意,请把符合题意的选项填在下表中)
-
1.下列图形中,可以由其中一个图形通过平移得到的是( )
组卷:586引用:22难度:0.7 -
2.下列运算中,正确的是( )
组卷:844引用:11难度:0.6 -
3.下列多项式中,能用平方差公式进行因式分解的是( )
组卷:246引用:5难度:0.7 -
4.若一个三角形的三边长分别为2、6、a,则a的值可以是( )
组卷:824引用:16难度:0.7 -
5.正多边形的一个内角为144°,那么该正多边形的边数为( )
组卷:398引用:7难度:0.9 -
6.如图,用三角板作△ABC的边AB上的高,下列三角板的摆放位置正确的是( )
组卷:168引用:4难度:0.5 -
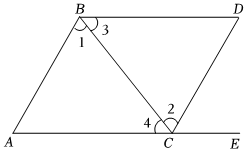 7.如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )组卷:2709引用:112难度:0.7
7.如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )组卷:2709引用:112难度:0.7 -
8.如图①,现有边长为b和a+b的正方形纸片各一张,长和宽分别为b、a的长方形纸片一张,其中a<b.把纸片Ⅰ、Ⅲ按图②所示的方式放入纸片Ⅱ内,已知图②中阴影部分的面积满足S1=8S2,则a,b满足的关系式为( )
 组卷:183引用:3难度:0.6
组卷:183引用:3难度:0.6
二、填空题(本大题共8小题,每小题3分,共24分,请把答案直接填在题中的横线上)
-
9.华为作为世界顶级科技公司,设计的麒麟90005GSoc芯片,拥有领先的5nm制程和架构设计,5nm=0.000000005m,数据0.000000005用科学记数法表示为 .
组卷:73引用:5难度:0.7
三、解答题(本题共11小题,共102分.解答应写出必要的计算过程、推演步骤或文字说明)
-
26.配方法是数学中重要的一种思想方法.它是指将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法.这种方法常被用到代数式的变形中,并结合非负数的意义来解决一些问题.我们定义:一个整数能表示成a2+b2(a、b是整数)的形式,则称这个数为“完美数”.例如,5是“完美数”.理由:因为5=22+12,所以5是“完美数”.
简单应用:
(1)已知41是“完美数”,请将它写成a2+b2(a、b是整数)的形式 ;
(2)若x2-8x+9可配方成(x-m)2+n(m、n为常数),则mn=;
深入探究:
(3)已知x2+y2-4x+2y+5=0,则x+y=;
灵活运用:
(4)已知S=x2+4y2+4x-12y+k(x、y是整数,k是常数),要使S为“完美数”,试求出符合条件的一个k值,并说明理由.组卷:194引用:1难度:0.5 -
27.学习概念:
规定①:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.
规定②:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.
理解概念:
(1)如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB,请根据规定①,写出图中所有的“等角三角形”;
(2)如图2,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,请根据规定②,求证:CD为△ABC的等角分割线;
应用概念:
(3)在△ABC中,∠A=42°,CD是△ABC的等角分割线,直接写出∠ACB的度数.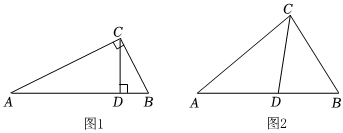 组卷:260引用:3难度:0.1
组卷:260引用:3难度:0.1


