2022-2023学年安徽省淮南市西部地区九年级（上）第二次联考数学试卷

一、选择题（本大题共10小题，每小题4分，共40分）

• 1．下列图形中，是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：293引用：16难度：0.9

  解析

• 2．x=1是关于x的一元二次方程x²+ax+2b=0的解，则2a+4b=（　　）

  A．-2

  B．-3

  C．-1

  D．-6
  组卷：4379引用：62难度：0.9

  解析

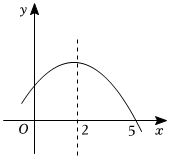• 3．如图所示的是二次函数y=ax²+bx+c的部分图象，由图象可知不等式ax²+bx+c＜0的解集是（　　）

  A．-1＜x＜5

  B．x＞5

  C．x＜-1且x＞5

  D．x＜-1或x＞5
  组卷：2068引用：34难度：0.5

  解析

• 4．如图，在△ABC中，以C为中心，将△ABC顺时针旋转35°得到△DEC，边ED，AC相交于点F，若∠A=30°，则∠EFC的度数为（　　）

  A．60°

  B．65°

  C．72.5°

  D．80°
  组卷：28引用：1难度：0.5

  解析

• 5．下表是一组二次函数y=x²+3x-5的自变量x与函数值y的对应值：
  

  x	1	1.1	1.2	1.3	1.4
  y	-1	-0.49	0.04	0.59	1.16

  那么方程x²+3x-5=0的一个近似根是（　　）

  A．1

  B．1.1

  C．1.2

  D．1.3
  组卷：458引用：9难度：0.6

  解析

• 6．已知抛物线y=-x²+bx+4经过（-2，n）和（4，n）两点，则n的值为（　　）

  A．-2

  B．-4

  C．2

  D．4
  组卷：9249引用：71难度：0.7

  解析

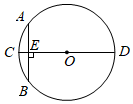• 7．如图，CD为⊙O的直径，弦AB⊥CD于E，OE=12，AB=10，那么直径CD的长为（　　）

  A．12.5

  B．13

  C．25

  D．26
  组卷：573引用：11难度：0.5

  解析

三、解答题（本大题共9小题，满分0分）

• 22．在△ABC中，AB=AC，∠BAC=α（0°＜α＜60°），将线段BC绕点B逆时针旋转60°得到线段BD．
  （1）如图1，直接写出∠ABD的大小（用含α的式子表示）；
  （2）如图2，∠BCE=150°，∠ABE=60°，判断△ABE的形状并加以证明；
  （3）在（2）的条件下，连接DE，若∠DEC=45°，求α的值．
  
  组卷：6002引用：101难度：0.4

  解析

• 23．如图，抛物线y=-

  1

  2

  x

  2

  +bx+c与x轴交于A，B（4，0）两点，与y轴交于点C，一次函数y=-

  1

  2

  x+n经过点B，C，点P是抛物线上的动点，过点P作PQ⊥x轴，垂足为Q，交直线BC于点D．
  （1）求抛物线的解析式及点A的坐标；
  （2）当点P位于直线BC上方且△PBC面积最大时，求线段PD的长；
  （3）是否存在点P，使得以P，D，O，C为顶点的四边形是平行四边形？若存在，请求出点P的坐标；若不存在，请说明理由．
  组卷：41引用：4难度：0.5

  解析