2021-2022学年湖北省荆州市沙市中学九年级（上）月考数学试卷（12月份）

一、选择题（本大题共10小题，每小题只有唯一正确答案，每小题3分，共30分）

• 1．如图是几种汽车轮毂的图案，图案绕中心旋转90°后能与原来的图案重合的是（　　）

  A．

  B．

  C．

  D．
  组卷：1768引用：15难度：0.5

  解析

• 2．已知方程x²-5x+2=0的两个解分别为x₁、x₂，则x₁x₂的值为（　　）

  A．5

  B．-5

  C．2

  D．-2
  组卷：167引用：2难度：0.8

  解析

• 3．如图图案中，不是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：91引用：4难度：0.8

  解析

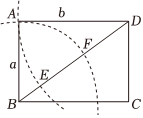• 4．如图，在矩形ABCD中，以点D为圆心，AD为半径作弧与BD交于点E，以点B为圆心，AB为半径作弧与BD交于点F．设AB=a,AD=b,则（　　）

  A．线段DF的长是方程x2+2ax=b2的一个解

  B．线段DF的长是方程x2-2ax=b2的一个解

  C．线段BE的长是方程x2+bx=a2的一个解

  D．线段BE的长是方程x2-bx=a2的一个解
  组卷：1172引用：3难度：0.5

  解析

• 5．抛物线y=x²先向左平移1个单位，再向上平移3个单位，得到的抛物线解析式是（　　）

  A．y=（x+1）2+3

  B．y=（x+1）2-3

  C．y=（x-1）2-3

  D．y=（x-1）2+3
  组卷：125引用：5难度：0.9

  解析

• 6．在平面直角坐标系中，抛物线y=（x+2）²-5关于y轴对称的抛物线所对应的函数关系式为（　　）

  A．y=（x+2）2-5．	B．y=（x-2）2-5
  C．y=-（x-2）2+5．	D．y=-（x+2）2+5
  组卷：52引用：1难度：0.6

  解析

• 7．下列事件中，属于必然事件的是（　　）

  A．任意买一张电影票，座位号是奇数

  B．太阳东升西落

  C．明天是晴天

  D．过马路时恰好遇到红灯
  组卷：116引用：7难度：0.8

  解析

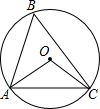• 8．如图，△ABC内接于⊙O，且∠ABC=70°，则∠AOC为（　　）

  A．140°

  B．120°

  C．90°

  D．35°
  组卷：42引用：4难度：0.7

  解析

• 9．将函数y=x²-4x+2化为y=a（x-h）²+k的形式正确的是（　　）

  A．y=（x-4）2+2

  B．y=（x-2）2-2

  C．y=（x-4）2-2

  D．y=（x-2）2+2
  组卷：351引用：4难度：0.7

  解析

• 10．如图，△ABC的内切圆⊙O与BC，CA，AB分别相切于点D，E，F．已知△ABC的周长为36，AB=9，BC=14，则AF的长为（　　）

  A．4

  B．5

  C．9

  D．13
  组卷：972引用：5难度：0.7

  解析

二、填空题（本大题共6小题，每小题3分，共18分）

• 11．某县2008年农民人均年收入为7 800元，计划到2010年，农民人均年收入达到9 100元．设人均年收入的平均增长率为x,则可列方程

  ．
  组卷：341引用：63难度：0.7

  解析

• 12．如表记录了一名球员在罚球线上投篮的结果．那么，这名球员投篮一次，投中的概率约为

  （精确到0.1）．
  

  投篮次数（n）	50	100	150	200	250	300	500
  投中次数（m）	28	60	78	104	123	152	251
  投中频率（m/n）	0.56	0.60	0.52	0.52	0.49	0.51	0.50
  组卷：2044引用：98难度：0.7

  解析

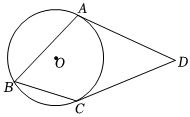• 13．如图，四边形ABCD的两边AD、CD与⊙O相切于A、C两点，点B在⊙O上，若∠D=50°，则∠B的度数为

  ．
  组卷：83引用：1难度：0.5

  解析

• 14．已知抛物线y=x²-x-1与x轴的一个交点为（m,0），则代数式-3m²+3m+2022的值为

  ．
  组卷：334引用：4难度：0.6

  解析

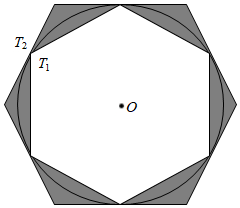• 15．如图，有一个⊙O和两个正六边形T₁，T₂．T₁的六个顶点都在圆周上，T₂的六条边都和⊙O相切（我们称T₁、T₂分别为⊙O的内接正六边形和外切正六边形）．设⊙O的半径为R，则图中阴影部分的面积

  （用含R的式子表示）．
  组卷：349引用：2难度：0.3

  解析

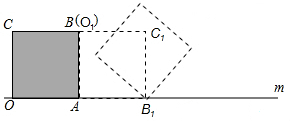• 16．把边长为1的正方形纸片OABC放在直线m上，OA边在直线m上，然后将正方形纸片绕着顶点A按顺时针方向旋转90°，此时，点O运动到了点O₁处（即点B处），点C运动到了点C₁处，点B运动到了点B₁处，又将正方形纸片AO₁C₁B₁绕B₁点，按顺时针方向旋转90°…，按上述方法经过4次旋转后，顶点O经过的总路程为

  ，经过61次旋转后，顶点O经过的总路程为

  ．
  组卷：826引用：56难度：0.7

  解析

三、解答题（本大题共8小题，共72分）

• 17．某宾馆有50个房间供游客住宿，当每个房间的房价为每天180元时，房间会全部住满．当每个房间每天的房价每增加10元时，就会有一个房间空闲．宾馆需对游客居住的每个房间每天支出20元的各种费用．根据规定，每个房间每天的房价不得高于340元．设每个房间的房价增加x元（x为10的正整数倍）．
  （1）设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围；
  （2）设宾馆一天的利润为w元，求w与x的函数关系式；
  （3）一天订住多少个房间时，宾馆的利润最大？最大利润是多少元？
  组卷：1356引用：52难度：0.3

  解析

• 18．已知关于x的一元二次方程2x²+（a+4）x+a=0．
  （1）求证：无论a为任何实数，此方程总有两个不相等的实数根；
  （2）抛物线

  C

  1

  ：

  y

  =

  2

  x

  2

  +

  （

  a

  +

  4

  ）

  x

  +

  a

  与x轴的一个交点的横坐标为

  a

  2

  ，其中a≠0，将抛物线C₁向右平移

  1

  4

  个单位，再向上平移

  1

  8

  个单位，得到抛物线C₂．求抛物线C₂的解析式；
  （3）点A（m,n）和B（n,m）都在（2）中抛物线C₂上，且A、B两点不重合，求代数式2m³-2mn+2n³的值．
  组卷：321引用：5难度：0.1

  解析

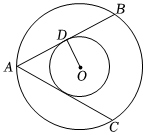• 19．如图，在两个同心圆O中，AB、AC都是大圆的弦，且AB=AC，AB与小圆相切于点D，则AC与小圆相切吗？请说明理由．
  组卷：57引用：1难度：0.6

  解析

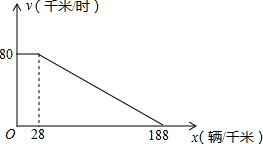• 20．“城市发展 交通先行”，成都市今年在中心城区启动了缓堵保畅的二环路高架桥快速通道建设工程，建成后将大大提升二环路的通行能力．研究表明，某种情况下，高架桥上的车流速度V（单位：千米/时）是车流密度x（单位：辆/千米）的函数，且当0＜x≤28时，V=80；当28＜x≤188时，V是x的一次函数．函数关系如图所示．
  （1）求当28＜x≤188时，V关于x的函数表达式；
  （2）若车流速度V不低于50千米/时，求当车流密度x为多少时，车流量P（单位：辆/时）达到最大，并求出这一最大值．
  （注：车流量是单位时间内通过观测点的车辆数，计算公式为：车流量=车流速度×车流密度）
  组卷：845引用：12难度：0.3

  解析

• 21．解方程：
  （1）x²-4x-12=0；
  （2）x（x-9）=8（9-x）．
  组卷：1365引用：6难度：0.6

  解析

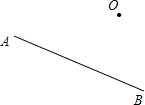• 22．如图，以点O为中心，把线段AB逆时针旋转90°．
  组卷：24引用：4难度：0.5

  解析

• 23．如图是一个量角器和一个含30°角的直角三角板放置在一起的示意图，其中点B在半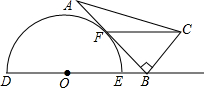圆O的直径DE的延长线上，AB切半圆O于点F，且BC=OE．
  （1）求证：DE∥CF；
  （2）当OE=2时，若以O，B，F为顶点的三角形与△ABC相似，求OB的长；
  （3）若OE=2，移动三角板ABC且使AB边始终与半圆O相切，直角顶点B在直径DE的延长线上移动，求出点B移动的最大距离．
  组卷：665引用：17难度：0.1

  解析

• 24．现有5个质地、大小完全相同的小球上分别标有数字-1，-2，1，2，3．先将标有数字-2，1，3的小球放在第一个不透明的盒子里，再将其余小球放在第二个不透明的盒子里．现分别从两个盒子里各随即取出一个小球．
  （1）请利用列表或画树状图的方法表示取出的两个小球上数字之和所有可能的结果；
  （2）求取出的两个小球上的数字之和等于0的概率．
  组卷：179引用：19难度：0.5

  解析