2023-2024学年江苏省扬州市广陵区八年级（上）月考数学试卷（10月份）

一、选择题（本大题共8小题，每小题3分，共24分）

• 1．围棋起源于中国，古代称之为“弈”，至今已有四千多年的历史．下列由黑、白棋子摆成的图案中，是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：521引用：17难度：0.8

  解析

• 2．下列说法正确的是（　　）

  A．完全重合的两个三角形全等

  B．面积相等的两个三角形全等

  C．所有的等边三角形全等

  D．形状相同的两个三角形全等
  组卷：364引用：128难度：0.9

  解析

• 3．在元旦联欢会上，3名小朋友分别站在△ABC三个顶点的位置上，他们在玩抢凳子游戏，要求在他们中间放一个木凳，谁先坐到凳子上谁获胜，为使游戏公平，则凳子应放置的最适当的位置时在△ABC的（　　）

  A．三边中线的交点	B．三条角平分线的交点
  C．三边垂直平分线的交点	D．三边上高的交点
  组卷：1630引用：40难度：0.7

  解析

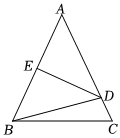• 4．如图，在△ABC中，AB=AC，AD=BD，DE⊥AB于点E，若BC=4，△BDC的周长为10，则AE的长为（　　）

  A．2.5

  B．3

  C．3.5

  D．4
  组卷：544引用：8难度：0.7

  解析

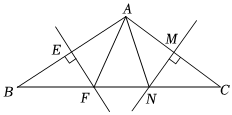• 5．如图，在△ABC中，∠BAC=110°，EF是边AB的垂直平分线，垂足为E，交BC于F．MN是边AC的垂直平分线，垂足为M，交BC于N．连接AF、AN，则∠FAN的度数是（　　）

  A．70°

  B．55°

  C．40°

  D．30°
  组卷：1046引用：7难度：0.7

  解析

• 6．如图a是长方形纸带，∠DEF=25°，将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是（　　）
  

  A．105°

  B．120°

  C．125°

  D．130°
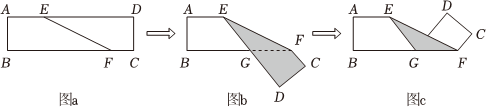  组卷：254引用：4难度：0.7

  解析

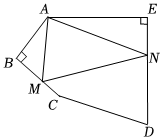• 7．如图，在五边形ABCDE中，∠BAE=120°，∠B=∠E=90°，AB=BC，AE=DE，在BC、DE上分别找到一点M、N，使得△AMN的周长最小值，则∠AMN+∠ANM的度数为（　　）

  A．100°

  B．110°

  C．120°

  D．130°
  组卷：318引用：4难度：0.5

  解析

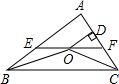• 8．如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列四个结论：①∠BOC=90°+

  1

  2

  ∠A，②∠EBO=

  1

  2

  ∠AEF，③∠DOC+∠OCB=90°，④设OD=m,AE+AF=n,则S_△AEF=

  mn

  2

  ．其中正确的结论有（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：980引用：8难度：0.6

  解析

二、填空题（本大题共10小题，每小题3分，共30分）请把答案直接填写在横线上

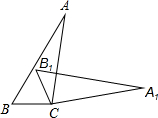• 9．如图，△ABC≌△A₁B₁C₁，且∠A：∠B：∠ACB=1：3：5，则∠A₁等于

   

  度．
  组卷：161引用：2难度：0.5

  解析

三.解答题（本大题共10小题，共96分）.解答时应写出文字说明、证明过程或演算步骤.

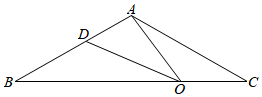• 27．如图，△ABC中，AB=AC，∠B=30°，点O在BC边上运动（O不与B、C重合），点D在线段AB上，连结AO，OD．点O运动时，始终满足∠AOD=∠B．
  （1）当OD∥AC时，判断△AOB的形状并说明理由；
  （2）当AO的最小值为2时，此时BD=

  ；
  （3）在点O的运动过程中，△AOD的形状是等腰三角形时，请直接写出此时∠BDO的度数．
  组卷：257引用：4难度：0.2

  解析

• 28．已知在△ABC中，AB=AC，过点B引一条射线BM，D是BM上一点．
  【问题解决】
  （1）如图1，若∠ABC=60°，射线BM在∠ABC内部，∠ADB=60°，求证：∠BDC=60°．小明同学展示的做法是：在BM上取一点E使得AE=AD．通过已知的条件，从而求得∠BDC的度数，请你帮助小明写出证明过程：
  【类比探究】
  （2）如图2，已知∠ABC=∠ADB=30°．
  ①当射线BM在∠ABC内，求∠BDC的度数；
  ②当射线BM在BC下方，如图3所示，请问∠BDC的度数会变化吗？若不变，请说明理由，若改变，请求出∠BDC的度数．
  
  组卷：608引用：7难度：0.3

  解析