当前位置：试卷中心 > 试卷详情

2020-2021学年河南省开封二十七中八年级（下）月考数学试卷（3月份）

发布：2025/11/23 1:0:8

一、选择题（本大题共10个小题，每小题3分，共30分.）

1．如图中的一块砖的宽AN=5cm,长ND=10cm,CD上的点B距地面的高度BD=8cm.地面上A处的一只蚂蚁要到B处吃食，需爬行的最短路径是（　　）cm.
A．15 B．16 C．17 D．23
组卷：217引用：1难度：0.5
2．如图，将矩形ABCD的四个角向内折叠铺平，恰好拼成一个无缝隙无重叠的矩形EFGH，若EH=5，EF=12，则CD长为（　　）
A．13 B．
120
13
C．12 D．17
组卷：409引用：2难度：0.3
3．计算
12
（
75
+3
1
3
-
48
）的结果是（　　）
A．6 B．4
3
C．2
3
+6 D．12
组卷：545引用：18难度：0.9
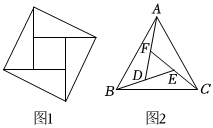4．大约在公元222年，赵爽为《周髀算经》一书作序时，介绍了“勾股圆方图”，亦称“赵爽弦图”（如图1），某数学兴趣小组类比“赵爽弦图”构造出图2：△ABC为等边三角形，AD、BE、CF围成的△DEF也是等边三角形．已知点D、E、F分别是BE、CF、AD的中点，若△ABC的面积为14，则△DEF的面积是（　　）
A．1 B．2 C．3 D．4
组卷：766引用：12难度：0.5
5．在平行四边形ABCD中，∠B+∠D=120°，则∠A等于（　　）
A．60° B．75° C．120° D．130°
组卷：55引用：2难度：0.5
6．下列二次根式中，是最简二次根式的是（　　）
A．
18
B．
a
2
b
C．
0
.
5
D．
x
2
+
1
组卷：538引用：1难度：0.9
7．如图，将△ABC沿DE折叠，使点A与BC边的中点F重合，下列结论中正确的是（　　）
A．EF∥AB且EF=
1
2
AB B．∠BAF=∠CAF
C．S_{四边形ADFE}=AF•DE D．∠BDF+∠FEC=2∠BAC
组卷：20引用：1难度：0.9
8．一个三角形的三边之比为5：12：13，它的周长为60，则它的面积是（　　）
A．120 B．144 C．196 D．60
组卷：448引用：7难度：0.7
9．如图，在四边形ABCD中，AB∥DC，要使四边形ABCD是平行四边形，下列可添加的条件不正确的是（　　）
A．AD=BC B．AB=CD C．AD∥BC D．∠A=∠C
组卷：217引用：5难度：0.7
10．如图1，已知DE是△ABC的中位线，求证：DE∥BC，
DE
=
1
2
BC
．嘉嘉根据图2，把下面打乱的证明步骤进行了整理，你认为正确的证明排序是（　　）
①又∵
DE
=
1
2
DF

②∴四边形ADCF是平行四边形，∴CF∥DA，CF=DA
③∴DE∥BC，
DE
=
1
2
BC

④延长DE到F，使EF=DE，连接FC，DC，AF
⑤∵AE=EC，EF=DE
⑥∴CF∥BD，CF=BD，∴四边形DBCF是平行四边形，∴DF∥BC，DF=BC
A．④③②①⑥⑤ B．④⑤②⑥①③ C．④⑤③⑥②① D．④⑤①②⑥③
组卷：66引用：1难度：0.5

二、填空题（本大题共5小题，每小题3分，满分15分）

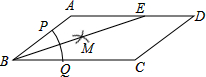11．如图，在▱ABCD中，AB=3，BC=5，以点B的圆心，以任意长为半径作弧，分别交BA、BC于点P、Q，再分别以P、Q为圆心，以大于
1
2
PQ的长为半径作弧，两弧在∠ABC内交于点M，连接BM并延长交AD于点E，则DE的长为
．
组卷：3835引用：27难度：0.5
12．如果式子
x
-
4
有意义，那么x的取值范围是
．
组卷：247引用：14难度：0.8
13．如图，在△ABC中，AB=3，BC=4，∠B=90°，若将△ABC折叠，使C点与A点重合，则FC的长为
．
组卷：11引用：1难度：0.6
14．已知x,y为实数，且
x
-
1
+3（y-2）²=0，则
x
y
的值为

．
组卷：119引用：6难度：0.7
15．如图，2×2的方格中，小正方形的边长是1，点A、B、C都在格点上，则△ABC中AB边上的高长为

．
组卷：265引用：3难度：0.7

三、解答题（本大题共8小题，共55分）

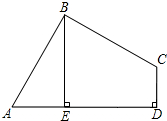16．已知：如图，在四边形ABCD中，∠ABC=90°，CD⊥AD，AD²+CD²=2AB²．
（1）求证：AB=BC；
（2）当BE⊥AD于E时，试证明：BE=AE+CD．
组卷：6894引用：22难度：0.5
17．阅读材料，黑白双雄，纵横江湖；双剑合壁，天下无敌．这是武侠小说中的常见描述，其意是指两个人合在一起，团结一致、优势互补、取长补短、威力无比，在二次根式中也有这种相辅相成的“对子”．如：
（
5
+
3
）
（
5
-
3
）
=
-
4
，像
（
5
+
3
）
和
（
5
-
3
）
这样的两个二次根式，它们的积不含根号，我们就称这两个二次根式互为有理化因式，其中一个是另一个的有理化因式．再如
（
3
+
2
）
与
（
3
-
2
）
也互为有理化因式．于是，下面二次根式除法可以这样运算：
2
+
3
2
-
3
=
（
2
+
3
）
（
2
+
3
）
（
2
-
3
）
（
2
+
3
）
=
7
+
4
3
，像这样，通过分子、分母同乘以一个式子把分母中的根号化去的过程叫分母有理化，解决问题．
（1）
2
3
+
3
2
的一个有理化因式是
，
4
3
-
5
分母有理化结果是
．
（2）计算：
1
2
+
1
+
1
3
+
2
+
1
2
+
3
．
（3）比较大小：
7
-
5

15
-
13
．
组卷：90引用：1难度：0.5
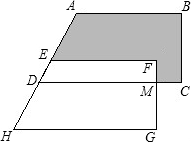18．将直角梯形ABCD平移得梯形EFGH，若HG=10，MC=2，MG=4，求图中阴影部分的面积．
组卷：479引用：5难度：0.5
19．如图所示，点D是等腰Rt△ABC的斜边BC上一动点，连接AD，作等腰Rt△ADE，使AD=AE，且∠DAE=90°连接BE、CE．
（1）判断BD与CE的数量关系与位置关系，并进行证明；
（2）当四边形ADCE的周长最小值是6时，求BC的值．
组卷：764引用：2难度：0.5
20．计算：
（
1
2
）
-
1
-（-1）²⁰⁰⁸-（π-3）⁰+
12
．
组卷：801引用：17难度：0.5
21．如图，在▱ABCD中，点E是CD的中点，AE的延长线与BC的延长线相交于点F．
（1）求证：△ADE≌△FCE；
（2）连接AC、DF，判断四边形ACFD是什么四边形？说明理由．
组卷：145引用：1难度：0.3
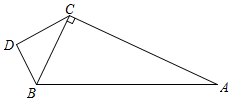22．如图，在Rt△ABC中，∠BCA=90°，AC=12，AB=13，点D是Rt△ABC外一点，连接DC，DB，且CD=4，BD=3．
（1）求BC的长；
（2）求证：△BCD是直角三角形．
组卷：7974引用：56难度：0.8
23．先观察下列等式，再回答问题
①
1
+
1
1
2
+
1
2
2
=
1
+
1
1
-
1
1
+
1
=
1
1
2

②
1
+
1
2
2
+
1
3
2
=
1
+
1
2
-
1
2
+
1
=
1
1
6

③
1
+
1
3
2
+
1
4
2
=
1
+
1
3
-
1
3
+
1
=
1
1
12

（1）根据上面三个等式，请猜想
1
+
1
4
2
+
1
5
2
的结果（直接写出结果）
（2）根据上述规律，解答问题：设m=
1
+
1
1
2
+
1
2
2
+
1
+
1
2
2
+
1
3
2
+
1
+
1
3
2
+
1
4
2
+…+
1
+
1
2019
2
+
1
2020
2
，求不超过m的最大整数是多少？
组卷：422引用：3难度：0.7

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．EF∥AB且EF= 1 2 AB	B．∠BAF=∠CAF
C．S_{四边形ADFE}=AF•DE	D．∠BDF+∠FEC=2∠BAC

2020-2021学年河南省开封二十七中八年级（下）月考数学试卷（3月份）

一、选择题（本大题共10个小题，每小题3分，共30分.）

1．如图中的一块砖的宽AN=5cm,长ND=10cm,CD上的点B距地面的高度BD=8cm.地面上A处的一只蚂蚁要到B处吃食，需爬行的最短路径是（ ）cm.

2．如图，将矩形ABCD的四个角向内折叠铺平，恰好拼成一个无缝隙无重叠的矩形EFGH，若EH=5，EF=12，则CD长为（ ）

3．计算12（75+313-48）的结果是（ ）

5．在平行四边形ABCD中，∠B+∠D=120°，则∠A等于（ ）

6．下列二次根式中，是最简二次根式的是（ ）

7．如图，将△ABC沿DE折叠，使点A与BC边的中点F重合，下列结论中正确的是（ ）

8．一个三角形的三边之比为5：12：13，它的周长为60，则它的面积是（ ）

9．如图，在四边形ABCD中，AB∥DC，要使四边形ABCD是平行四边形，下列可添加的条件不正确的是（ ）

二、填空题（本大题共5小题，每小题3分，满分15分）

11．如图，在▱ABCD中，AB=3，BC=5，以点B的圆心，以任意长为半径作弧，分别交BA、BC于点P、Q，再分别以P、Q为圆心，以大于12PQ的长为半径作弧，两弧在∠ABC内交于点M，连接BM并延长交AD于点E，则DE的长为．

12．如果式子x-4有意义，那么x的取值范围是．

13．如图，在△ABC中，AB=3，BC=4，∠B=90°，若将△ABC折叠，使C点与A点重合，则FC的长为 ．

14．已知x,y为实数，且x-1+3（y-2）2=0，则xy的值为 ．

15．如图，2×2的方格中，小正方形的边长是1，点A、B、C都在格点上，则△ABC中AB边上的高长为 ．

三、解答题（本大题共8小题，共55分）

16．已知：如图，在四边形ABCD中，∠ABC=90°，CD⊥AD，AD2+CD2=2AB2．（1）求证：AB=BC；（2）当BE⊥AD于E时，试证明：BE=AE+CD．

18．将直角梯形ABCD平移得梯形EFGH，若HG=10，MC=2，MG=4，求图中阴影部分的面积．

19．如图所示，点D是等腰Rt△ABC的斜边BC上一动点，连接AD，作等腰Rt△ADE，使AD=AE，且∠DAE=90°连接BE、CE．（1）判断BD与CE的数量关系与位置关系，并进行证明；（2）当四边形ADCE的周长最小值是6时，求BC的值．

20．计算：（12）-1-（-1）2008-（π-3）0+12．

21．如图，在▱ABCD中，点E是CD的中点，AE的延长线与BC的延长线相交于点F．（1）求证：△ADE≌△FCE；（2）连接AC、DF，判断四边形ACFD是什么四边形？说明理由．

22．如图，在Rt△ABC中，∠BCA=90°，AC=12，AB=13，点D是Rt△ABC外一点，连接DC，DB，且CD=4，BD=3．（1）求BC的长；（2）求证：△BCD是直角三角形．

1．如图中的一块砖的宽AN=5cm,长ND=10cm,CD上的点B距地面的高度BD=8cm.地面上A处的一只蚂蚁要到B处吃食，需爬行的最短路径是（　　）cm.

2．如图，将矩形ABCD的四个角向内折叠铺平，恰好拼成一个无缝隙无重叠的矩形EFGH，若EH=5，EF=12，则CD长为（　　）

3．计算
12
（
75
+3
1
3
-
48
）的结果是（　　）

5．在平行四边形ABCD中，∠B+∠D=120°，则∠A等于（　　）

6．下列二次根式中，是最简二次根式的是（　　）

7．如图，将△ABC沿DE折叠，使点A与BC边的中点F重合，下列结论中正确的是（　　）

8．一个三角形的三边之比为5：12：13，它的周长为60，则它的面积是（　　）

9．如图，在四边形ABCD中，AB∥DC，要使四边形ABCD是平行四边形，下列可添加的条件不正确的是（　　）

11．如图，在▱ABCD中，AB=3，BC=5，以点B的圆心，以任意长为半径作弧，分别交BA、BC于点P、Q，再分别以P、Q为圆心，以大于
1
2
PQ的长为半径作弧，两弧在∠ABC内交于点M，连接BM并延长交AD于点E，则DE的长为
．

12．如果式子
x
-
4
有意义，那么x的取值范围是
．

13．如图，在△ABC中，AB=3，BC=4，∠B=90°，若将△ABC折叠，使C点与A点重合，则FC的长为
．

14．已知x,y为实数，且
x
-
1
+3（y-2）²=0，则
x
y
的值为

．

15．如图，2×2的方格中，小正方形的边长是1，点A、B、C都在格点上，则△ABC中AB边上的高长为

．

16．已知：如图，在四边形ABCD中，∠ABC=90°，CD⊥AD，AD²+CD²=2AB²．
（1）求证：AB=BC；
（2）当BE⊥AD于E时，试证明：BE=AE+CD．

19．如图所示，点D是等腰Rt△ABC的斜边BC上一动点，连接AD，作等腰Rt△ADE，使AD=AE，且∠DAE=90°连接BE、CE．
（1）判断BD与CE的数量关系与位置关系，并进行证明；
（2）当四边形ADCE的周长最小值是6时，求BC的值．

20．计算：
（
1
2
）
-
1
-（-1）²⁰⁰⁸-（π-3）⁰+
12
．

21．如图，在▱ABCD中，点E是CD的中点，AE的延长线与BC的延长线相交于点F．
（1）求证：△ADE≌△FCE；
（2）连接AC、DF，判断四边形ACFD是什么四边形？说明理由．

22．如图，在Rt△ABC中，∠BCA=90°，AC=12，AB=13，点D是Rt△ABC外一点，连接DC，DB，且CD=4，BD=3．
（1）求BC的长；
（2）求证：△BCD是直角三角形．