2022-2023学年江西省赣州市章贡区某校八年级（上）第一次月考数学试卷

一．选择题（本大题6小题，每小题3分，共18分）

• 1．如果一个三角形两边长为2cm和5cm,则第三边长可能为（　　）

  A．2cm

  B．3cm

  C．4cm

  D．8cm
  组卷：237引用：2难度：0.6

  解析

• 2．下列计算结果正确的是（　　）

  A．a2•a3=a6

  B．a5÷a=a5

  C．（a3）2=a6

  D．（ab2）3=ab6
  组卷：27引用：2难度：0.7

  解析

• 3．若x²+2kx+64是一个完全平方式，则k的值是（　　）

  A．8

  B．±8

  C．16

  D．±16
  组卷：326引用：6难度：0.8

  解析

• 4．下列各组图形中，BD是△ABC的高的图形是（　　）

  A．

  B．

  C．

  D．
  组卷：2937引用：22难度：0.7

  解析

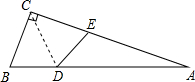• 5．如图，△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A=22°，则∠EDA等于（　　）

  A．44°

  B．68°

  C．46°

  D．77°
  组卷：301引用：9难度：0.7

  解析

• 6．如图，△AOB≌△ADC，点B和点C是对应顶点，∠O=∠D=90°，记∠OAD=α，∠ABO=β，∠ABC=∠ACB，当BC∥OA时，α与β之间的数量关系为（　　）

  A．α=β

  B．α=2β

  C．α+β=90°

  D．α+2β=180°
  组卷：723引用：7难度：0.7

  解析

二．填空题（本大题6小题，每小题3分，共18分）

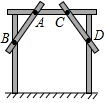• 7．如图所示，王师傅做完门框为防止变形，在门上钉上AB、CD两条斜拉的木条，其中的数学原理是

  ．
  组卷：551引用：22难度：0.6

  解析

五．（本大题2小题，每小题9分，共18分）

• 22．定义：如果三角形的两个内角α与β满足α+2β=100°，那么我们称这样的三角形为“奇妙三角形”．
  （1）如图1，△ABC中，∠ACB=80°，BD平分∠ABC．
  求证：△ABD为“奇妙三角形”
  （2）若△ABC为“奇妙三角形”，且∠C=80°．求证：△ABC是直角三角形；
  （3）如图2，△ABC中，BD平分∠ABC，若△ABD为“奇妙三角形”，且∠A=40°，直接写出∠C的度数．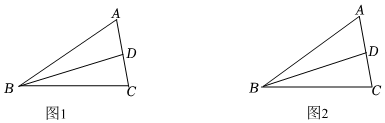
  
  组卷：1228引用：5难度：0.5

  解析

六．解答题（本大题共12分）

• 23．（1）问题背景：如图1，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E，F分别是BC，CD上的点，且∠EAF=60°，探究图中线段BE，EF，FD之间的数量关系，小王同学探究此问题的方法是，延长FD到点G．使DG=BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是

  ；
  （2）探索延伸：如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°，E，F分别是BC，CD上的点，且∠BAD=2∠EAF，上述结论是否仍然成立，并说明理由；
  （3）实际应用：如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以50海里/小时的速度前进，舰艇乙沿北偏东50°的方向以65海里/小时的速度前进，前进3小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离．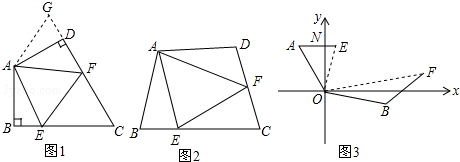
  
  组卷：284引用：5难度：0.1

  解析