2023年海南省儋州市部分校中考数学模拟试卷（二）

一、选择题。(本大题满分36分,每小题3分)在下列各题的四个备选答案中,有且只有一个是正确的,请在答题卡上把你认为正确的答案的字母代号按要求用2B铅笔涂黑）

• 1．-3的绝对值是（　　）

  A．3

  B． 1 3

  C． - 1 3

  D．-3
  组卷：3414引用：660难度：0.9

  解析

• 2．海南省发布的《关于促进海南文体会展活动恢复振兴的若干措施》中提到，设立文体专项奖补资金，总规模1.1亿元，其中60000000元用于支持市县政府、企业和社会力量举办文体活动．数据60000000用科学记数法表示为 （　　）

  A．6×106

  B．60×106

  C．6×107

  D．0.6×108
  组卷：10引用：2难度：0.8

  解析

• 3．若代数式2x+1的值为5，则x等于 （　　）

  A．3

  B．2

  C．-2

  D．-3
  组卷：178引用：2难度：0.9

  解析

• 4．如图是由5个相同的正方体搭成的几何体，这个几何体的主视图是（　　）

  A．

  B．

  C．

  D．
  组卷：103引用：6难度：0.9

  解析

• 5．某学校在“喜迎二十大，永远跟党走”的征文比赛中，随机抽查20名同学的成绩，如下表所示：

  人数/名	3	4	5	8
  成绩/分	92	93	95	97

  则本组数据的中位数和众数分别是（　　）

  A．94，95

  B．96，97

  C．95，95

  D．95，97
  组卷：35引用：2难度：0.7

  解析

• 6．下列计算中，正确的是（　　）

  A．a3+a2=a5	B．（a3）3=a6
  C．（-ab）2=-a2b2	D．a6÷a2=a4
  组卷：26引用：2难度：0.7

  解析

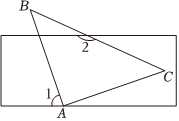• 7．如图，等腰直角三角形ABC的直角顶点A落在矩形纸片的一边上，若∠1=70°，则∠2的度数为（　　）

  A．155°

  B．145°

  C．120°

  D．105°
  组卷：17引用：2难度：0.7

  解析

三、解答题。(本大题满分72分)

• 21．在边长为4的正方形ABCD中，对角线AC，BD相交于点O，点P为对角线BD上一动点，连接AP，以AP为斜边在直线AP的上方构造等腰直角三角形AQP，连接OQ．
  （1）如图1，当点P与点B重合时．
  求证：①△AOD≌AQB；
  ②四边形ADOQ是平行四边形；
  （2）如图2，当点P在线段OB上时（不与点O，B重合），猜想∠AOQ的度数是否为定值，若是，求出∠AOQ的度数，若不是，请说明理由；
  （3）如图3，当BA=BP时，求点Q到线段AB的距离．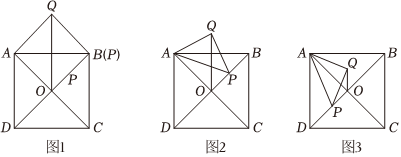
  ​
  组卷：68引用：2难度：0.1

  解析

• 22．如图1，抛物线y=ax²+bx+3与x轴交于点A（-3，0），B（1，0），与y轴交于点C，对称轴直线x=m交抛物线于点D，交x轴于点E，连接AD，CD．
  （1）求该抛物线的表达式以及m的值；
  （2）求四边形OADC的面积；
  （3）如图2，作直线AC，点P为对称轴左侧抛物线上一动点，点Q为直线AC上一动点．
  ①连接BQ，OQ，求BQ+OQ的最小值；
  ②若以点C，D，P，Q为顶点的四边形为平行四边形，直接写出点Q的坐标．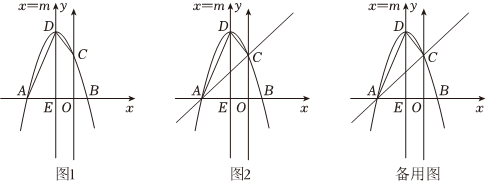
  ​
  组卷：103引用：2难度：0.3

  解析