2023年云南省保山市中考数学模拟试卷（4月份）

一、选择题（本大题共12小题，每小题只有一个正确选项，每小题3分，共36分）

• 1．一个化学实验小组人员分别做测量锌跟盐酸反应生成氢气的实验：5人分别称取锌块6.51克，6.52克，6.49克，6.50克，6.48克，生成的氢气用排水法收集，测得分别为：2.25升，2.26升，2.23升，2.24升，2.22升，则由此实验得出的氢气的密度为（　　）

  A．8.9×10-5克/厘米3	B．8.9×10-4克/厘米3
  C．8.9×10-3克/厘米3	D．8.9×10-2克/厘米3
  组卷：199引用：1难度：0.5

  解析

• 2．不等式组

  2 x - 1 ＜ 3

  x ＞ - 1

  的解集是（　　）

  A．x＜2

  B．x＞-1

  C．-1＜x＜2

  D．无解
  组卷：89引用：17难度：0.9

  解析

• 3．桌上放着一个茶壶，4个同学从各自的方向观察，请指出实物图右边的四幅图，从左至右分别是由哪个同学看到的（　　）
  

  A．①②③④

  B．①③②④

  C．②④①③

  D．④③①②
  组卷：91引用：25难度：0.9

  解析

• 4．△ABC的三边之比为3：4：5，若△ABC∽△A′B′C′，且△A′B′C′的最短边长为6，则△A′B′C′的周长为（　　）

  A．36

  B．24

  C．18

  D．12
  组卷：569引用：22难度：0.9

  解析

• 5．用科学记数法表示2350000正确的是（　　）

  A．235×104

  B．2.35×106

  C．2.35×105

  D．2.35×104
  组卷：90引用：6难度：0.7

  解析

• 6．观察下列数的规律：2、4、8、16、32、…，则第6个数是（　　）

  A．56

  B．64

  C．80

  D．128
  组卷：170引用：3难度：0.9

  解析

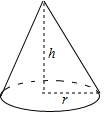• 7．如图，圆锥的底面半径r=6，高h=8，则圆锥的侧面积是（　　）

  A．15π

  B．30π

  C．45π

  D．60π
  组卷：2164引用：12难度：0.5

  解析

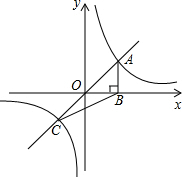• 8．若函数y=kx（k＞0）与函数

  y

  =

  1

  x

  的图象相交于A，C两点，AB垂直x轴于B，则△ABC的面积为（　　）

  A．1

  B．2

  C．k

  D．k2
  组卷：1910引用：8难度：0.9

  解析

• 9．已知x₁，x₂是一元二次方程x²+2x-3=0的两根，则x₁+x₂，x₁x₂的值分别为（　　）

  A．-2，3

  B．2，3

  C．3，-2

  D．-2，-3
  组卷：77引用：8难度：0.7

  解析

• 10．下列运算一定正确的是（　　）

  A．2a+a=2a2	B．a2•a4=a6
  C．（3a3）2=6a6	D．（a+b）2=a2+b2
  组卷：40引用：1难度：0.9

  解析

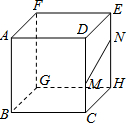• 11．如图，正方体的棱长为3，点M，N分别在CD，HE上，CM=

  1

  2

  DM，HN=2NE，HC与NM的延长线交于点P，则tan∠NPH的值为（　　）

  A． 1 2

  B．2

  C． 1 3

  D． 2 3
  组卷：144引用：2难度：0.9

  解析

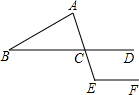• 12．如图，直线BD∥EF，AE与BD交于点C，若∠ABC=30°，∠BAC=75°，则∠CEF的大小为（　　）

  A．60°

  B．75°

  C．90°

  D．105°
  组卷：143引用：16难度：0.9

  解析

二、填空题（本大题共4小题，每小题2分，共8分）

• 13．-0.1的相反数是

   

  ，倒数是

   

  ，绝对值是

   

  ．
  组卷：14引用：1难度：0.9

  解析

• 14．△ABC中，AD⊥BC于D，∠ACD=60°，若AD=2

  3

  ，AB=2

  7

  ，则BC=

  ．
  组卷：243引用：1难度：0.5

  解析

• 15．若正多边形的每一个内角为135°，则这个正多边形的边数是

  ．
  组卷：2416引用：54难度：0.7

  解析

• 16．把多项式2a²-4ab+2b²分解因式的结果是

   

  ．
  组卷：181引用：37难度：0.9

  解析

三、解答题（本大题共8小题，共56分）

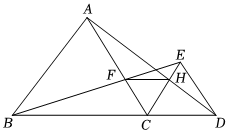• 17．如图．已知点B、C、D在同一条直线上．△ABC和△CDE都是等边三角形，BE交AC于F，AD交CE于H．
  （1）求证：△BCE≌△ACD；
  （2）求证：CF=CH；
  （3）判断FH与BD的位置关系，并证明．
  组卷：186引用：1难度：0.3

  解析

• 18．计算：（-2）²-

  8

  •

  1

  2

  +（sin60°-π）⁰．
  组卷：164引用：52难度：0.7

  解析

• 19．某中学举行秋季田径运动会，赛事共有三项：A．“赛跑”、B．“投掷”、C．“跳远”．小明和小刚参与了该运动会的志愿者服务工作，组委会随机将志愿者分配到三个项目组．
  （1）小明被分配到“赛跑”项目组的概率为

  ；
  （2）求小明和小刚被分配到不同项目组的概率．
  组卷：23引用：1难度：0.5

  解析

• 20．如图，在△ABC中，∠ACB=90°，点D为AB的中点，过点D作AB的垂线交BC于点E，过点A作AF∥BE交ED的延长线于点F，连结AE，BF．
  （1）求证：四边形AEBF是菱形．
  （2）若sin∠EBF=

  4

  5

  ，AE=5，
  ①求四边形ACBF的周长．
  ②连结CD，求CD的长．
  组卷：519引用：2难度：0.5

  解析

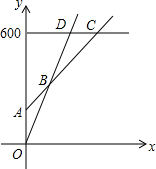• 21．某游泳馆普通票价20元/张，暑假为了促销，新推出两种优惠卡：
  ①金卡售价600元/张，每次凭卡不再收费．
  ②银卡售价150元/张，每次凭卡另收10元．
  暑假普通票正常出售，两种优惠卡仅限暑假使用，不限次数．设游泳x次时，所需总费用为y元
  （1）分别写出选择银卡、普通票消费时，y与x之间的函数关系式；
  （2）在同一坐标系中，若三种消费方式对应的函数图象如图所示，请求出点A、B、C的坐标；
  （3）请根据函数图象，直接写出选择哪种消费方式更合算．
  组卷：10761引用：100难度：0.5

  解析

• 22．2022年是我国航天事业辉煌的一年，神舟十四号和神舟十五号两个飞行乘组6位航天员在太空会师，在神州大地上掀起了航天热潮．某学校为了解学生对我国航天事业的知晓情况，在全校范围内开展了航天知识竞赛，学校随机抽取了50名学生的成绩，整理并绘制了如下不完整的频数分布表和频数分布直方图．
  50名学生竞赛成绩频数分布直方表​
  

  组别	成绩	频数	百分比
  第1组	40≤x＜50	2	4%
  第2组	50≤x＜60	a	10%
  第3组	60≤x＜70	18	36%
  第4组	70≤x＜80	9	18%
  第5组	80≤x＜90	b	m%
  第6组	90≤x＜100	2	4%
  合计		50	100%

  其中第3组数据如下：
  61，62，62，63，64，64，64，64，64，64，64，64，64，64，66，67，67，69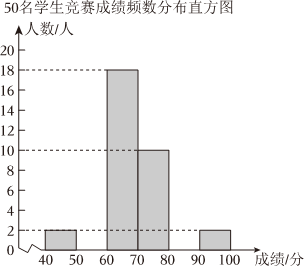
  请根据以上信息解答下列问题：
  （1）频数分布直方表中a=

  ，b=

  ，m=

  ；
  （2）请直接在图中补全频数分布直方图；
  （3）抽取的第3组学生竞赛成绩的众数是

  ；
  （4）若该校共有1000名学生，请估算该校航天知识竞赛成绩不低于80分的学生共有

  人．
  组卷：18引用：1难度：0.5

  解析

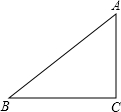• 23．在△ABC中，如图，∠C=90°，AC=6，BC=8，设直线l与斜边AB交于点E，与直角边交于点F．设AE=x,是否存在直线l同时平分△ABC的周长和面积？若存在直线l,求出x的值；若不存在直线l,请说明理由．
  组卷：36引用：1难度：0.5

  解析

• 24．如图（1），直线y=-x+3与x轴、y轴分别交于点B、点C，经过B、C两点的抛物线y=x²+bx+c与x轴的另一个交点为A，顶点为P．
  （1）求该抛物线的解析式；
  （2）在该抛物线的对称轴上是否存在点M，使以C、P、M为顶点的三角形为等腰三角形？若存在，请直接写出所有符合条件的点M的坐标；若不存在，请说明理由；
  （3）连接AC，在x轴上是否存在点Q，使以P、B、Q为顶点的三角形与△ABC相似？若存在，请求出点Q的坐标；若不存在，请说明理由；
  （4）当0＜x＜3时，在抛物线上求一点E，使△CBE的面积有最大值．
  （图（2）、图（3）供画图探究）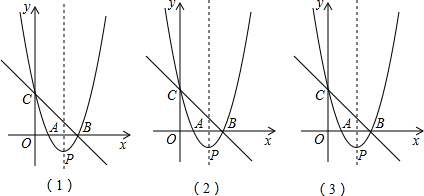
  
  组卷：630引用：8难度：0.1

  解析