当前位置：试卷中心 > 试卷详情

2023年湖南省衡阳市衡州中学中考数学一模试卷

发布：2025/11/21 3:0:8

一、选择题（本大题共12个小题，每小题3分，满分36分．在每小题给出的四个选项中，只有一项是符合题目要求的．）

1．下列图形中，既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
组卷：23引用：2难度：0.8
2．疫情期间，某快递公司推出无接触配送服务，第1周接到5万件订单，第2周到第3周订单量增长率是第1周到第2周订单量增长率的1.5倍，若第3周接到订单为7.8万件，设第1周到第2周的订单增长率为x,可列得方程为（　　）
A．5（1+x+1.5x）=7.8 B．5（1+x×1.5x）=7.8
C．5（1+x）（1+1.5x）=7.8 D．7.8（1-x）（1-1.5x）=5
组卷：32引用：4难度：0.8
3．下面计算中，正确的是（　　）
A．（-2mn）³=8m³n³ B．（m+n）³（m+n）²=m⁵+n⁵
C．-（a³b²）³=-a⁹b⁶ D．（-
1
3
a⁴b）²=
1
6
a⁶b²
组卷：80引用：2难度：0.7
4．下列命题是假命题的有（　　）
①对顶角相等，②直线外的一点到这条直线的垂线段叫做点到直线的距离，③过一点有且只有一条直线与已知直线平行，④两条直线被第三条直线所截，同旁内角互补．
A．1个 B．2个 C．3个 D．4个
组卷：226引用：4难度：0.6
5．若一个数的相反数不是正数，则这个数一定是（　　）
A．正数 B．正数或0 C．负数 D．负数或0
组卷：367引用：9难度：0.9
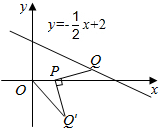6．如图，在平面直角坐标系中，Q是直线y=-
1
2
x+2上的一个动点，将Q绕点P（1，0）顺时针旋转90°，得到点Q'，连接OQ'，则OQ'的最小值为（　　）
A．
4
5
5
B．
5
C．
5
2
3
D．
6
5
5
组卷：5479引用：37难度：0.6
7．把不等式组
x
-
2
≥
0
x
+
1
＜
0
的解集表示在数轴上，正确的是（　　）
A． B． C． D．
组卷：190引用：49难度：0.9
8．函数y=
1
x
-
3
+（x-5）^-2中自变量x的取值范围是（　　）
A．x≥3且x≠5 B．x＞3且x≠5 C．x＜3且x≠5 D．x≤3且x≠5
组卷：2594引用：7难度：0.7
9．下列立体图形中，侧面展开图是扇形的是（　　）
A． B． C． D．
组卷：1800引用：98难度：0.9
10．若
（
a
-
3
）
2
=
a
-
3
，则a的取值范围是（　　）
A．a＞3 B．a≥3 C．a＜3 D．a≤3
组卷：1248引用：35难度：0.9
11．今年初，党中央、国务院对湖北发生的新型冠状病毒肺炎疫情非常重视，共派遣援鄂抗疫医务人员42000多人，经过全国人民的共同努力，取得了这场战疫的胜利：42000这个数用科学记数法表示为（　　）
A．42×10³ B．4.2×10⁴ C．4.2×10⁵ D．4.2×10³
组卷：78引用：2难度：0.9
12．下列关系式中，不是y关于x的反比例函数的是（　　）
A．xy=2 B．y=
5
x
8
C．x=
5
7
y
D．x=5y^-1
组卷：960引用：2难度：0.8

二、填空题（本大题共6个小题，每小题3分，满分18分．）

13．等边△ABC，AB=8，点D在直线AB上，若CD=13，则AD的长为
．
组卷：482引用：4难度：0.5
14．如图，两个形状为正十边形的纪念币一边重合放置在一起，则∠α=
度．
组卷：150引用：3难度：0.9
15．如图1，在第一个天平上，物块A的质量等于物块B加上物块C的质量；如图2，在第二个天平上，物块A加上物块B的质量等于3个物块C的质量．已知物块A的质量为10g.请你判断：1个物块B的质量是
g.
组卷：275引用：2难度：0.5
16．如图，AB∥CD，EG平分∠AEN，若∠EFD=108°，则∠GEN的度数为
．
组卷：96引用：2难度：0.6
17．（a+
9
-
4
a
a
-
2
）÷
a
2
-
9
a
-
2
=
．
组卷：742引用：2难度：0.7
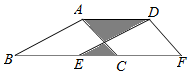18．如图，△ABC的边长AB=3cm,BC=4cm,AC=2cm,将△ABC沿BC方向平移a cm（a＜4），得到△DEF，连接AD，则阴影部分的周长为
cm.
组卷：1011引用：14难度：0.5

三、解答题（木大题共8个小题，19～20题每题6分，21～24题每题8分，25题10分，26题12分，满分66分．解答应写出文字说明、证明过程或演算步骤．）

19．一个多边形的内角和是外角和的2倍，求这个多边形的边数及对角线的条数．
组卷：73引用：2难度：0.5
20．如图，已知二次函数y=ax²+
3
2
x+c的图象与y轴交于点A（0，4），与x轴交于点B、C，点C坐标为（8，0），连接AB、AC．
（1）请直接写出二次函数y=ax²+
3
2
x+c的表达式；
（2）判断△ABC的形状，并说明理由；
（3）若点N在x轴上运动，当以点A、N、C为顶点的三角形是等腰三角形时，请直接写出此时点N的坐标；
（4）若点N在线段BC上运动（不与点B、C重合），过点N作NM∥AC，交AB于点M，当△AMN面积最大时，求此时点N的坐标．
组卷：4852引用：62难度：0.5
21．八（1）班同学为了解2015年某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据进行如下整理，
月均用水量x（t）频数（户）频率
0＜x≤5 6 0.12
5＜x≤10 m 0.24
10＜x≤15 16 0.32
15＜x≤20 10 0.20
20＜x≤25 4 n
60≤x＜70 2 0.04
请解答以下问题：
（1）填空：m=

，n=

，并把频数分布直方图补充完整；
（2）若该小区有1000户家庭，求该小区月均用水量超过10t的家庭大约有多少户？
组卷：145引用：1难度：0.5
22．计算：
（1）（x+3）²-（x-2）（x+3）
（2）
1
a
+
1
-
a
+
1
a
2
-
2
a
+
1
÷
a
+
1
a
-
1
．
组卷：168引用：1难度：0.1
23．第三届亚洲沙滩运动会服务中心要在某校选拔一名志愿者．经笔试、面试，结果小明和小颖并列第一．评委会决定通过抓球来确定人选．抓球规则如下：在不透明的布袋里装有除颜色之外均相同的2个红球和1个绿球，小明先取出一个球，记住颜色后放回，然后小颖再取出一个球．若取出的球都是红球，则小明胜出；若取出的球是一红一绿，则小颖胜出．你认为这个规则对双方公平吗？请用列表法或画树状图的方法进行分析．
组卷：100引用：7难度：0.7
24．阅读下列材料，并解答后面的问题．
在学习了直角三角形的边角关系后，小颖和小明两个学习小组继续探究任意锐角三角形的边角关系：在锐角△ABC中，∠A、∠B、∠C的对边分别是a、b、c.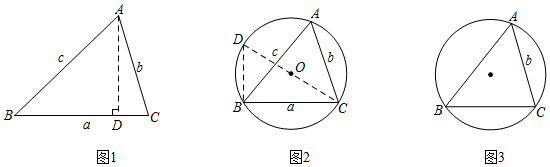

（1）小明学习小组发现如下结论：
如图1，过A作AD⊥BC于D，则sinB=
AD
c
，sinC=
AD
b
，即AD=csinB，AD=bsinC，于是
=
，即
b
sin
B
=
c
sin
C
，同理有
c
sin
C
=
a
sin
A
，
a
sin
A
=
b
sin
B
，
则有
a
sin
A
=
b
sin
B
=
c
sin
C
．
（2）小颖学习小组则利用圆的有关性质也得到了类似的结论：
如图2，△ABC的外接圆半径为R，连接CO并延长交⊙O于点D，连接DB，则∠D=∠A，
∵CD为⊙O的直径，
∴∠DBC=90°，
在Rt△DBC中，
∵sinD=
BC
DC
=
a
2
R
，
∴sinA=
a
2
R
，即
a
sin
A
=2R，
同理：
b
sin
B
=2R，
c
sin
C
=2R，
则有
a
sin
A
=
b
sin
B
=
c
sin
C
=2R，
请你将这一结论用文字语言描述出来：
．
小颖学习小组在证明过程中略去了“
b
sin
B
=2R，
c
sin
C
=2R”的证明过程，请你把“
b
sin
B
=2R，”的证明过程补写出来．
（3）直接用前面阅读材料中得出的结论解决问题
规划局为了方便居民，计划在三个住宅小区A、B、C之间修建一座学校，使它到三个住宅小区的距离相等，已知小区C在小区B的正东方向
3
千米处，小区A在小区B的东北方向，且A与C之间相距
2
千米，求学校到三个小区的距离及小区A在小区C的什么方向？
组卷：305引用：2难度：0.4
25．如图，我国某边防哨所树立了“祖国在我心中”建筑物，它的横截面为四边形BCNM，其中BC⊥CN，BM∥CN，建筑物顶上有一旗杆AB，士兵小明站在D处，由E点观察到旗杆顶部A的仰角为52°，底部B的仰角为45°，已知旗杆AB=2.8米，DE=1.8米．
（参考数据：sin52°≈0.788，tan52°≈1.280）
（1）求建筑物的高度BC；
（2）建筑物长50米，背风坡MN的坡度i=1：0.5，为提高建筑物抗风能力，士兵们在背风坡填筑土石方加固，加固后建筑物顶部加宽4.2米，背风坡GH的坡度为i=1：1.5，施工10天后，边防居民为士兵支援的机械设备终于到达，这样工作效率提高到了原来的2倍，结果比原计划提前20天完成加固任务，士兵们原计划平均每天填筑土石方多少立方米？
组卷：293引用：3难度：0.5
26．如图，在△ABC中，AB=AC，以AB为直径的圆O交AC于点D，交BC于点E，以点B为顶点作∠CBF，使得∠CBF=
1
2
∠BAC，交AC延长线于点F连接BD、AE，延长AE交BF于点G，
（1）求证：BF为⊙O的切线；
（2）求证：AC•BC=BD•AG；
（3）若BC=2
10
，CD：CF=4：5，求⊙O的半径．
组卷：1489引用：3难度：0.2

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．5（1+x+1.5x）=7.8	B．5（1+x×1.5x）=7.8
C．5（1+x）（1+1.5x）=7.8	D．7.8（1-x）（1-1.5x）=5

A．（-2mn）³=8m³n³	B．（m+n）³（m+n）²=m⁵+n⁵
C．-（a³b²）³=-a⁹b⁶	D．（- 1 3 a⁴b）²= 1 6 a⁶b²

月均用水量x（t）	频数（户）	频率
0＜x≤5	6	0.12
5＜x≤10	m	0.24
10＜x≤15	16	0.32
15＜x≤20	10	0.20
20＜x≤25	4	n
60≤x＜70	2	0.04

2023年湖南省衡阳市衡州中学中考数学一模试卷

一、选择题（本大题共12个小题，每小题3分，满分36分．在每小题给出的四个选项中，只有一项是符合题目要求的．）

1．下列图形中，既是轴对称图形又是中心对称图形的是（ ）

2．疫情期间，某快递公司推出无接触配送服务，第1周接到5万件订单，第2周到第3周订单量增长率是第1周到第2周订单量增长率的1.5倍，若第3周接到订单为7.8万件，设第1周到第2周的订单增长率为x,可列得方程为（ ）

3．下面计算中，正确的是（ ）

4．下列命题是假命题的有（ ）①对顶角相等，②直线外的一点到这条直线的垂线段叫做点到直线的距离，③过一点有且只有一条直线与已知直线平行，④两条直线被第三条直线所截，同旁内角互补．

5．若一个数的相反数不是正数，则这个数一定是（ ）

6．如图，在平面直角坐标系中，Q是直线y=-12x+2上的一个动点，将Q绕点P（1，0）顺时针旋转90°，得到点Q'，连接OQ'，则OQ'的最小值为（ ）

7．把不等式组x-2≥0x+1＜0的解集表示在数轴上，正确的是（ ）

8．函数y=1x-3+（x-5）-2中自变量x的取值范围是（ ）

9．下列立体图形中，侧面展开图是扇形的是（ ）

10．若（a-3）2=a-3，则a的取值范围是（ ）

11．今年初，党中央、国务院对湖北发生的新型冠状病毒肺炎疫情非常重视，共派遣援鄂抗疫医务人员42000多人，经过全国人民的共同努力，取得了这场战疫的胜利：42000这个数用科学记数法表示为（ ）

12．下列关系式中，不是y关于x的反比例函数的是（ ）

二、填空题（本大题共6个小题，每小题3分，满分18分．）

13．等边△ABC，AB=8，点D在直线AB上，若CD=13，则AD的长为．

14．如图，两个形状为正十边形的纪念币一边重合放置在一起，则∠α=度．

15．如图1，在第一个天平上，物块A的质量等于物块B加上物块C的质量；如图2，在第二个天平上，物块A加上物块B的质量等于3个物块C的质量．已知物块A的质量为10g.请你判断：1个物块B的质量是 g.

16．如图，AB∥CD，EG平分∠AEN，若∠EFD=108°，则∠GEN的度数为．

17．（a+9-4aa-2）÷a2-9a-2=．

18．如图，△ABC的边长AB=3cm,BC=4cm,AC=2cm,将△ABC沿BC方向平移a cm（a＜4），得到△DEF，连接AD，则阴影部分的周长为 cm.

三、解答题（木大题共8个小题，19～20题每题6分，21～24题每题8分，25题10分，26题12分，满分66分．解答应写出文字说明、证明过程或演算步骤．）

19．一个多边形的内角和是外角和的2倍，求这个多边形的边数及对角线的条数．

22．计算：（1）（x+3）2-（x-2）（x+3）（2）1a+1-a+1a2-2a+1÷a+1a-1．

1．下列图形中，既是轴对称图形又是中心对称图形的是（　　）

2．疫情期间，某快递公司推出无接触配送服务，第1周接到5万件订单，第2周到第3周订单量增长率是第1周到第2周订单量增长率的1.5倍，若第3周接到订单为7.8万件，设第1周到第2周的订单增长率为x,可列得方程为（　　）

3．下面计算中，正确的是（　　）

4．下列命题是假命题的有（　　）
①对顶角相等，②直线外的一点到这条直线的垂线段叫做点到直线的距离，③过一点有且只有一条直线与已知直线平行，④两条直线被第三条直线所截，同旁内角互补．

5．若一个数的相反数不是正数，则这个数一定是（　　）

6．如图，在平面直角坐标系中，Q是直线y=-
1
2
x+2上的一个动点，将Q绕点P（1，0）顺时针旋转90°，得到点Q'，连接OQ'，则OQ'的最小值为（　　）

7．把不等式组
x
-
2
≥
0
x
+
1
＜
0
的解集表示在数轴上，正确的是（　　）

8．函数y=
1
x
-
3
+（x-5）^-2中自变量x的取值范围是（　　）

9．下列立体图形中，侧面展开图是扇形的是（　　）

10．若
（
a
-
3
）
2
=
a
-
3
，则a的取值范围是（　　）

11．今年初，党中央、国务院对湖北发生的新型冠状病毒肺炎疫情非常重视，共派遣援鄂抗疫医务人员42000多人，经过全国人民的共同努力，取得了这场战疫的胜利：42000这个数用科学记数法表示为（　　）

12．下列关系式中，不是y关于x的反比例函数的是（　　）

13．等边△ABC，AB=8，点D在直线AB上，若CD=13，则AD的长为
．

14．如图，两个形状为正十边形的纪念币一边重合放置在一起，则∠α=
度．

15．如图1，在第一个天平上，物块A的质量等于物块B加上物块C的质量；如图2，在第二个天平上，物块A加上物块B的质量等于3个物块C的质量．已知物块A的质量为10g.请你判断：1个物块B的质量是
g.

16．如图，AB∥CD，EG平分∠AEN，若∠EFD=108°，则∠GEN的度数为
．

17．（a+
9
-
4
a
a
-
2
）÷
a
2
-
9
a
-
2
=
．

18．如图，△ABC的边长AB=3cm,BC=4cm,AC=2cm,将△ABC沿BC方向平移a cm（a＜4），得到△DEF，连接AD，则阴影部分的周长为
cm.

22．计算：
（1）（x+3）²-（x-2）（x+3）
（2）
1
a
+
1
-
a
+
1
a
2
-
2
a
+
1
÷
a
+
1
a
-
1
．