2023-2024学年江苏省南通市崇川区启秀中学九年级（上）月考数学试卷（9月份）

一、单选题

• 1．如图，在⊙O中，直径CD垂直弦AB于点E，连接OB、CB，已知⊙O的半径为2，AB=

  2

  3

  ，则∠BCD的大小为（　　）

  A．30°

  B．45°

  C．60°

  D．15°
  组卷：167引用：7难度：0.9

  解析

• 2．二次函数y=x²-4x+7的最小值为（　　）

  A．2

  B．-2

  C．3

  D．-3
  组卷：1115引用：14难度：0.9

  解析

• 3．正六边形的边长为6cm,则该正六边形的内切圆面积为（　　）

  A．48πcm2

  B．36πcm2

  C．24πcm2

  D．27πcm2
  组卷：393引用：3难度：0.7

  解析

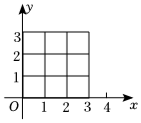• 4．如图，抛物线y=x²-mx+m+1恰好经过网格区域（含边界）中的2个格点（网格线的交点），则整数m的个数为（　　）

  A．3

  B．4

  C．5

  D．6
  组卷：241引用：2难度：0.5

  解析

• 5．已知⊙O的半径为10cm,点P到圆心O的距离为8cm,则点P和圆的位置关系（　　）

  A．点在圆内

  B．点在圆外

  C．点在圆上

  D．无法判断
  组卷：204引用：4难度：0.8

  解析

• 6．若⊙O₁与⊙O₂相切，它们的半径分别为3和8，则以下关于这两圆的圆心距O₁O₂的结论正确的是（　　）

  A．O1O2=5

  B．O1O2=11

  C．O1O2=5或11

  D．5＜O1O2＜11
  组卷：3引用：1难度：0.9

  解析

• 7．下列函数中，是二次函数的是（　　）

  A．y=x2- 1 x

  B．y=2x2+3x

  C．y=-x2+y2

  D．y=x+1
  组卷：119引用：5难度：0.9

  解析

• 8．关于抛物线y=2（x+3）²，以下说法正确的是（　　）

  A．开口向下

  B．对称轴是直线x=-3

  C．顶点坐标是（0，0）

  D．当x＞-3时，y随x增大而减小
  组卷：546引用：3难度：0.7

  解析

• 9．如图，直线l与⊙O相切于点A，M是⊙O上的个动点，MH⊥l,垂足为H．若⊙O的半径为1，则MA-MH的最大值为（　　）

  A．. 1 2

  B．. 1 3

  C．. 1 4

  D． 1 5
  组卷：63引用：1难度：0.5

  解析

• 10．如图，弧BE是半径为6的圆D的

  1

  4

  圆周，C点是

  ˆ

  BE

  上的任意一点，△ABD是等边三角形，则四边形ABCD的周长P的取值范围是（　　）

  A．12＜P≤18

  B．18＜P≤24

  C．18＜P≤18+6 2

  D．12＜P≤12+6 2
  组卷：765引用：33难度：0.9

  解析

二、填空题

• 11．二次函数y=-（x-6）²+8的最大值是

  ．
  组卷：2430引用：21难度：0.6

  解析

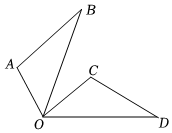• 12．如图，将△AOB绕着点O顺时针旋转，得到△COD，若∠AOB=45°，∠BOD=60°，则∠BOC=

  ．
  组卷：127引用：2难度：0.5

  解析

• 13．用反证法证明命题“三角形中至少有一个内角大于或等于60°“，应假设

  ．
  组卷：435引用：3难度：0.6

  解析

• 14．若抛物线y=2（x-2）²+k过原点，则该抛物线与x轴的另一个交点坐标为

   

  ．
  组卷：190引用：6难度：0.7

  解析

• 15．已知抛物线y=ax²+3ax+c（a≠0），若抛物线恒在x轴下方，且符合条件的整数a只有三个，则实数c的最小值为

  ．
  组卷：285引用：2难度：0.4

  解析

• 16．已知圆锥的侧面积为15πcm²，底面半径为3cm,则圆锥的高是

  ．
  组卷：441引用：46难度：0.7

  解析

• 17．图中圆心角∠AOB=30°，弦CA∥OB，延长CO与圆交于点D，则∠BOD=

  ．
  组卷：394引用：62难度：0.7

  解析

• 18．已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，有下列5个结论：
  ①abc＞0；②b＜a+c；③4a+2b+c＞0；④2c＜3b；⑤a+b＞m（am+b），（m≠1的实数）．
  其中正确的结论有

  ．（填序号）
  组卷：1868引用：35难度：0.7

  解析

三、解答题

• 19．已知扇形AOB的圆心角为240°，其面积为8cm²．求扇形AOB所在的圆的面积．
  组卷：65引用：1难度：0.5

  解析

• 20．如图，在平面直角坐标系中，抛物线y=ax²+bx+c与⊙M相交于A、B、C、D四点，其中A、B两点的坐标分别为（-1，0），（0，-2），点D在x轴上且AD为⊙M的直径．点E是⊙M与y轴的另一个交点，过劣弧

  ˆ

  ED

  上的点F作FH⊥AD于点H，且FH=1.5
  （1）求点D的坐标及该抛物线的表达式；
  （2）若点P是x轴上的一个动点，试求出△PEF的周长最小时点P的坐标；
  （3）在抛物线的对称轴上是否存在点Q，使△QCM是等腰三角形？如果存在，请直接写出点Q的坐标；如果不存在，请说明理由．
  组卷：2559引用：52难度：0.5

  解析

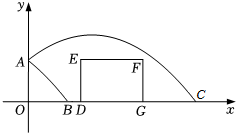• 21．如图，抛物线AB，AC是某喷水器喷出的水抽象而成，抛物线AB由抛物线AC向左平移得到，把汽车横截面抽象为矩形DEFG，其中DE=

  4

  3

  米，DG=2米，OA=h米，抛物线AC表达式为y=a（x-2）²+h+

  2

  3

  ，且点A，B，D，G，C均在坐标轴上．
  （1）若h=

  4

  3

  ，求抛物线AC表达式．
  （2）在条件（1）下，要使喷水器喷出的水能洒到整个汽车，记OD长为d米，求d的取值范围．
  （3）若h=1，喷水器喷出的水能否洒到整个汽车？请说明理由．
  组卷：417引用：5难度：0.3

  解析

• 22．已知二次函数y=x²-2x-3．
  （1）完成表格，并在平面直角坐标系中画出这个函数的图象．
  

  x	…	-1	0	1	2	3	…
  y	…			-4			…

  （2）结合图象回答：
  ①不等式x²-2x-3＜0的解集是

  ；
  ②当0≤x≤3时，y的取值范围是

  ；
  （3）直接写出不等式x²-2x-3＞-x-1的解集是

  ．
  
  组卷：34引用：2难度：0.5

  解析

• 23．平面直角坐标系xOy中，抛物线G：y=ax²+bx+c（a＞0）过点A（-1，c-3a），B（x₁，2），C（x₂，2）．顶点D不在第二象限，线段BC上有一点E，设△OBE的面积为S₁，△OCE的面积为S₂，S₁=S₂+1．
  （1）求抛物线G的对称轴；
  （2）求点E的坐标；
  （3）若抛物线G与直线DE的另一个交点F的横坐标为

  -

  4

  a

  -

  2

  ，求y=ax²+bx+c在-3＜x＜6时的取值范围（用含a的式子表示）．
  组卷：248引用：2难度：0.3

  解析

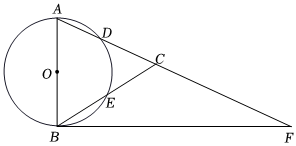• 24．如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠BAC=2∠CBF．
  （1）求证：BF是⊙O的切线；
  （2）若CF=8，BF=12，求圆的半径．
  组卷：42引用：2难度：0.6

  解析

• 25．如图，四边形ABCD内接于⊙O，∠BAD=90°，

  ˆ

  BC

  =

  ˆ

  CD

  ，过点C作CE⊥AD，垂足为E，若AE=3，DE=

  3

  ，求∠ABC的度数．
  组卷：1491引用：3难度：0.1

  解析

• 26．（1）如图1，△ABC中，∠C=90°，请用直尺和圆规作一条直线，把△ABC分割成两个等腰三角形（不写作法，但须保留作图痕迹）．
  （2）已知内角度数的两个三角形如图2，图3所示．请你判断，能否分别画一条直线把它们分割成两个等腰三角形？若能，请写出分割成的两个等腰三角形顶角的度数．
  
  组卷：602引用：21难度：0.3

  解析