2021-2022学年河北省保定市易县七年级（下）期中数学试卷

一、选择题（本大题有16个小题，共42分．1～10小题各3分，11～16小题各2分．在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．已知点P（-4，5），Q（-2，5），则直线PQ（　　）

  A．平行于x轴	B．平行于y轴
  C．垂直于x轴	D．以上都不正确
  组卷：278引用：4难度：0.8

  解析

• 2．能说明命题“对于任何实数a,|a|＞-a”是假命题的一个反例可以是（　　）

  A．a=1

  B．a= 2

  C．a= 1 3

  D．a=-2
  组卷：256引用：9难度：0.7

  解析

• 3．下列说法中不正确的是（　　）

  A．-2是4的平方根

  B． 3 8 是8的立方根

  C．立方根等于它本身的数只有1和0

  D．平方根等于它本身的数只有0
  组卷：67引用：3难度：0.9

  解析

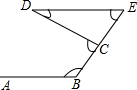• 4．如图所示，把一根铁丝折成图示形状后，AB∥DE，则∠BCD等于（　　）

  A．∠D+∠B

  B．∠B-∠D

  C．180°+∠D-∠B

  D．180°+∠B-∠D
  组卷：238引用：11难度：0.9

  解析

• 5．如图所示图案中，能看成是由一个基本图案经过平移得到的（　　）

  A．

  B．

  C．

  D．
  组卷：97引用：4难度：0.7

  解析

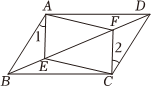• 6．如图，平行四边形ABCD中，E，F是对角线BD上的两点，如果添加一个条件使四边形AECF是平行四边形，则添加的条件不能是（　　）

  A．AE=CF

  B．BE=FD

  C．BF=DE

  D．∠1=∠2
  组卷：4693引用：21难度：0.5

  解析

• 7．在平面直角坐标系中，点A（4，-1）在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：59引用：6难度：0.9

  解析

• 8．如图，两直线相交于一点，若∠1+∠3=80°，则∠2=（　　）

  A．80°

  B．100°

  C．120°

  D．140°
  组卷：83引用：3难度：0.9

  解析

• 9．

  4

  的算术平方根是（　　）

  A．-2

  B．±2

  C． 2

  D．2
  组卷：2863引用：62难度：0.9

  解析

• 10．已知∠α=35°，则∠α的余角的度数是（　　）

  A．55°

  B．45°

  C．145°

  D．135°
  组卷：57引用：6难度：0.9

  解析

• 11．若一个角的补角的余角是28°，则这个角的度数为（　　）

  A．128°

  B．118°

  C．72°

  D．62°
  组卷：65引用：5难度：0.9

  解析

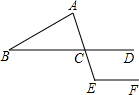• 12．如图，直线BD∥EF，AE与BD交于点C，若∠ABC=30°，∠BAC=75°，则∠CEF的大小为（　　）

  A．60°

  B．75°

  C．90°

  D．105°
  组卷：143引用：16难度：0.9

  解析

• 13．下列图形中，直线a与直线b平行的是（　　）

  A．

  B．

  C．

  D．
  组卷：80引用：2难度：0.9

  解析

• 14．下列各数中正数是（　　）

  A．2

  B．- 1 2

  C．0

  D．- 2
  组卷：94引用：54难度：0.9

  解析

• 15．电影院里的座位按“×排×号”编排，小明的座位简记为（8，6），小菲的位置简记为（8，12），则小明与小菲应坐在（　　）的位置上．

  A．同一排	B．前后同一条直线上
  C．中间隔六个人	D．前后隔六排
  组卷：781引用：8难度：0.9

  解析

• 16．下列各式化简结果为无理数的是（　　）

  A． 3 - 27

  B． （ 2 - 1 ） 0

  C． 8

  D． （ - 2 ） 2
  组卷：532引用：63难度：0.9

  解析

二、填空题（本大题有3个小题，每小题有两个空，每空2分，共12分）

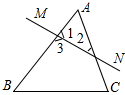• 17．如图，按角的位置关系填空：∠A与∠1是

   

  ；∠A与∠3是

   

  ；∠2与∠3是

   

  ．
  组卷：3093引用：14难度：0.7

  解析

• 18．已知x=

  2015

  -1，则（x+1）²+10的平方根是

  ．
  组卷：637引用：1难度：0.7

  解析

• 19．已知点P（3a-8，a-1），若点P在x轴上，则点P的坐标为

   

  ．
  组卷：80引用：3难度：0.9

  解析

三、解答题（本大题有7个小题，共66分，解答应写出文字说明、证明过程或演算步骤）

• 20．已知：如图，AB∥CD，∠ACD=2∠BAE．
  （1）若∠CAE=36°，求∠BAE的度数；
  （2）若点P在线段BA的延长线上，AF是∠PAC的角平分线，试说明：AF⊥AE．
  组卷：1131引用：1难度：0.5

  解析

• 21．如图，公路旁有两个高度相等的路灯AB、CD，小明上午上学时发现路灯AB在太阳光下的影子恰好落在路牌底部E处，他自己的影子恰好落在路灯CD的底部C处；晚自习放学时，站在上午同一个地方，发现在路灯CD的灯光下自己的影子恰好落在E处．
  （1）在图中画出小明的位置（用线段FG表示）．
  （2）若上午上学时，高1米的木棒的影子为2米，小明身高为1.5米，他距离路牌底部E恰好2米，求路灯高．
  组卷：322引用：4难度：0.5

  解析

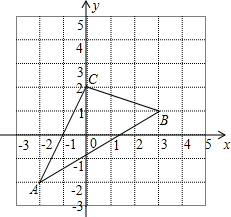• 22．如图，三角形ABC在平面直角坐标系中，
  （1）请写出三角形ABC各顶点的坐标；
  （2）若把三角形ABC向上平移3个单位，再向右平移2个单位得到三角形A'B'C'，写出点A'、B'、C'的坐标，并在坐标系中画出平移后的三角形；
  （3）求出三角形ABC的面积．
  组卷：141引用：2难度：0.7

  解析

• 23．如图，点E是线段BC的中点，分别以B、C为直角顶点的△EAB和△EDC均是等腰三角形，且在BC同侧．
  （1）AE和ED的数量关系为

  ；AE和ED的位置关系为

  ；
  （2）在图1中，以点E为位似中心，作△EGF与△EAB位似，点H是BC所在直线上的一点，连接GH，HD．分别得到图2和图3．
  ①在图2中，点F在BE上，△EGF与△EAB的相似比1：2，H是EC的中点．求证：GH=HD，GH⊥HD．
  ②在图3中，点F在的BE延长线上，△EGF与△EAB的相似比是k：1，若BC=2，请直接写CH的长为多少时，恰好使GH=HD且GH⊥HD（用含k的代数式表示）．
  
  组卷：1920引用：15难度：0.5

  解析

• 24．完成下面证明：
  如图，已知∠1+∠2=180°，∠3=∠A，
  求证：∠ACB=∠4．
  证明：∵∠1+∠2=180°，∠1+∠DFE=180°，
  ∴∠2=∠DFE（

  ）
  ∴AB∥EF（

  ）
  ∴∠5=∠3（

  ）
  又∵∠3=∠A
  ∴∠5=∠A（

  ）
  ∴

  ∥

  （

  ）
  ∴∠ACB=∠4（

  ）
  组卷：303引用：2难度：0.7

  解析

• 25．如图，已知AB∥CD．
  （1）猜想图1、图2、图3中∠B，∠BED，∠D之间有什么关系？
  （2）请用等式表示出它们的关系，并选择其中一个说说理由．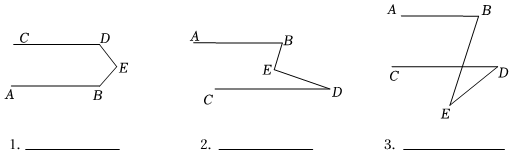
  组卷：27引用：1难度：0.5

  解析

• 26．计算：|-

  3

  |-（4-π）⁰+|

  3

  -2|
  组卷：136引用：1难度：0.7

  解析