2023年湖北省荆州市沙市区中考数学调研试卷（5月份）

一、选择题(本大题共10小题,每小题3分,共30分)

• 1．温度由-4℃上升7℃是（　　）

  A．3℃

  B．-3℃

  C．11℃

  D．-11℃
  组卷：2633引用：43难度：0.9

  解析

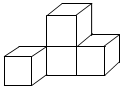• 2．如图是一个由4个相同正方体组成的立体图形，它的主视图是（　　）

  A．

  B．

  C．

  D．
  组卷：26引用：3难度：0.8

  解析

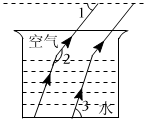• 3．如图，光在不同介质中的传播速度是不同的，因此当光线从水中射向空气时，要发生折射．由于折射率相同，所以在水中平行的光线在空气中也是平行的．如图，∠1=48°，∠2=158°，则∠3的度数为（　　）

  A．68°

  B．70°

  C．88°

  D．80°
  组卷：95引用：1难度：0.6

  解析

• 4．下列说法正确的是（　　）

  A．为了解近十年全国初中生的肥胖人数变化趋势，采用扇形统计图最合适

  B．“煮熟的鸭子飞了”是一个随机事件

  C．一组数据的中位数可能有两个

  D．为了解我省中学生的睡眠情况，应采用抽样调查的方式
  组卷：396引用：6难度：0.7

  解析

• 5．某气球内充满了一定质量m的气体，当温度不变时，气球内气体的气压p（单位：kPa）是气体体积V（单位：m³）的反比例函数：p=

  m

  V

  ，能够反映两个变量p和V函数关系的图象（　　）

  A．

  B．

  C．

  D．
  组卷：159引用：1难度：0.5

  解析

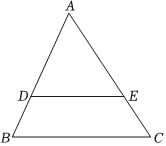• 6．如图，平行于BC的直线DE把△ABC分为面积相等的两部分，则DE：BC的值为 （　　）

  A．1：2

  B．2：3

  C． 2 ： 2

  D． 2 2 ： 2
  组卷：217引用：2难度：0.7

  解析

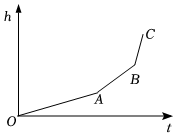• 7．匀速地向一个容器内注水，最后把容器注满．在注水过程中，水面高度h随时间t的变化规律如图所示（图中OABC为一折线）．这个容器的形状可能是（　　）

  A．

  B．

  C．

  D．
  组卷：2310引用：22难度：0.6

  解析

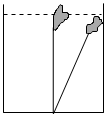• 8．《九章算术》勾股章有一“引葭赴岸”问题：“今有池方一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐．问：水深，葭长各几何．”意思是：如示意图，有一个水池，水面是一个边长为1丈的正方形，在水池正中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面，水的深度和芦苇的长度分别是多少？备注：1丈=10尺．设芦苇长x尺，水的深度为y尺，则可列方程为（　　）

  A．x2+102=（x+1）2	B．（x-1）2+52=x2
  C．y2+52=（y-1）2	D．y2+102=（x+1）2
  组卷：222引用：2难度：0.7

  解析

解答题(本大题共有8小题,共72分

• 23．问题背景
  如图（1），△ABD，△AEC都是等边三角形，△ACD可以由△AEB通过旋转变换得到，请写出旋转中心、旋转方向及旋转角的大小．
  尝试应用
  如图（2），在Rt△ABC中，∠ACB=90°，分别以AC，AB为边，作等边△ACD和等边△ABE，连接ED，并延长交BC于点F，连接BD．若BD⊥BC，求

  DF

  DE

  的值．
  拓展创新
  如图（3），在Rt△ABC中，∠ACB=90°，AB=2，将线段AC绕点A顺时针旋转90°得到线段AP，连接PB，直接写出PB的最大值．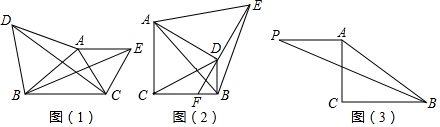
  
  组卷：4457引用：14难度：0.4

  解析

• 24．抛物线y=x²-4x与直线y=x交于原点O和点B，与x轴交于另一点A，顶点为D．
  （1）直接写出点B和点D的坐标；
  （2）如图1，连接OD，P为x轴上的动点，当tan∠PDO=

  1

  2

  时，求点P的坐标；
  （3）如图2，M是点B关于抛物线对称轴的对称点，Q是抛物线上的动点，它的横坐标为m（0＜m＜5），连接MQ，BQ，MQ与直线OB交于点E．设△BEQ和△BEM的面积分别为S₁和S₂，求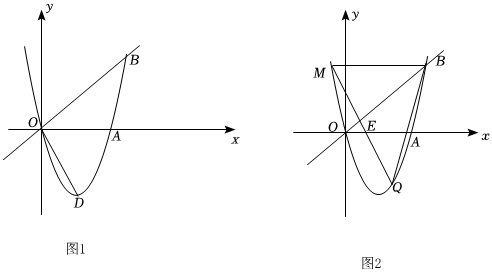

  S

  1

  S

  2

  的最大值．
  
  组卷：2519引用：7难度：0.2

  解析