2023-2024学年浙江省杭州市西湖区保俶塔申花实验学校八年级（上）月考数学试卷（10月份）

一、选择题（本大题共10小题，共30.0分）

• 1．若三角形两边长分别为2，6，则该三角形第三边长可能是（　　）

  A．3

  B．4

  C．5

  D．9
  组卷：446引用：9难度：0.6

  解析

• 2．如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（　　）

  A．

  B．

  C．

  D．
  组卷：19924引用：261难度：0.9

  解析

• 3．下列选项，可以用来证明命题“若a²＞b²，则a＞b”是假命题的反例是（　　）

  A．a=3，b=-2

  B．a=2，b=1

  C．a=-3，b=2

  D．a=-2，b=3
  组卷：400引用：7难度：0.8

  解析

• 4．根据下列已知条件，能作出唯一△ABC的是（　　）

  A．AB=3，BC=4，CA=8	B．AB=4，BC=3，∠A=60°
  C．∠A=60°，∠B=45°，AB=4	D．∠C=90°，∠B=30°，∠A=60°
  组卷：1744引用：14难度：0.7

  解析

• 5．如图是两个全等三角形，图中的字母表示三角形的边长，则∠1的度数为（　　）
  

  A．54°

  B．66°

  C．60°

  D．76°
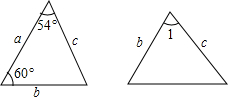  组卷：807引用：9难度：0.9

  解析

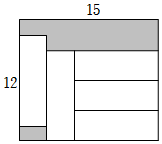• 6．如图，在长为15、宽为12的长方形中，有形状、大小完全相同的5个小长方形，则图中阴影部分的面积为（　　）

  A．65

  B．55

  C．45

  D．35
  组卷：526引用：4难度：0.8

  解析

• 7．如图，在△ABC中，∠C=90°，AC=8，DC=

  1

  3

  AD，BD平分∠ABC，则点D到AB的距离等于（　　）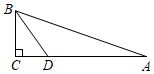
  

  A．4

  B．3

  C．2

  D．1
  组卷：4178引用：39难度：0.6

  解析

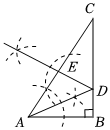• 8．如图，Rt△ABC中，∠ABC=90°，根据尺规作图的痕迹判断以下结论错误的是（　　）

  A．DB=DE

  B．AB=AE

  C．∠EDC=∠BAC

  D．∠DAC=∠C
  组卷：2859引用：45难度：0.5

  解析

三、解答题（本大题共8小题，共66.0分，解答应写出证明过程或演算步骤）

• 23．如图（1），AB=4cm,AC⊥AB，BD⊥AB，AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动．它们运动的时间为t（s）．
  （1）若点Q的运动速度与点P的运动速度相等，当t=1时，△ACP与△BPQ是否全等，并判断此时线段PC和线段PQ的位置关系，请分别说明理由；
  （2）如图（2），将图（1）中的“AC⊥AB，BD⊥AB”改为“∠CAB=∠DBA=60°”，其他条件不变．设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等？若存在，求出相应的x、t的值；若不存在，请说明理由．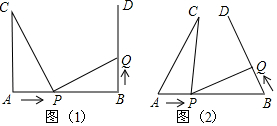
  
  组卷：14633引用：35难度：0.3

  解析

• 24．如图，∠BAD=∠CAE=90°，AB=AD，AE=AC，AF⊥CB，垂足为F．
  （1）求证：△ABC≌△ADE；
  （2）求∠FAE的度数；
  （3）求证：CD=2BF+DE．
  组卷：44294引用：76难度：0.1

  解析