当前位置：试卷中心 > 试卷详情

2023年黑龙江省佳木斯市抚远二中、三中中考数学三模试卷

发布：2024/6/16 8:0:10

一、选择题（每题3分，满分30分）

1．下列计算中，正确的是（　　）
A．a•a³=a⁴ B．a⁶÷a²=a³
C．（-2x²）³=-6x⁶ D．（a+2）²=a²+4
组卷：18引用：4难度：0.6
解析
2．如所示图形中，既是轴对称图形，又是中心对称图形的是（　　）
A． B． C． D．
组卷：125引用：4难度：0.9
解析
3．已知一组数据2，a,4，5的众数为5，则这组数据的平均数为（　　）
A．3 B．4 C．5 D．6
组卷：124引用：10难度：0.7
解析
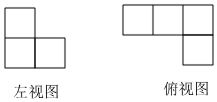4．如图是由一些完全相同的小正方体搭成的几何体的左视图和俯视图，搭成这个几何体所用的小正方体的个数至少是（　　）
A．3个 B．4个 C．5个 D．6个
组卷：272引用：5难度：0.7
解析
5．某种品牌运动服经过两次降价，每件零售价由1280元降为720元．已知两次降价的百分率都是x%，则x的值是（　　）
A．25% B．25 C．20% D．20
组卷：242引用：4难度：0.5
解析
6．已知关于x的分式方程
k
x
+
1
-
1
=
x
+
k
1
-
x
的解为负数，则k的取值范围是（　　）
A．
k
＞
-
1
2
B．
k
＜
-
1
2
且k≠-1
C．
k
＜
-
1
2
D．
k
＞
-
1
2
且k≠0
组卷：493引用：5难度：0.5
解析
7．装乒乓球的盒子有两种，大盒装6个，小盒装4个，若将50个乒乓球都装进盒子且把每个盒子都装满，那么不同的装球方法有（　　）
A．3种 B．4种 C．5种 D．6种
组卷：295引用：7难度：0.6
解析
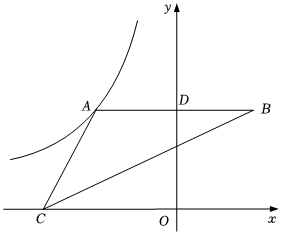8．如图，A是反比例函数y=
k
x
（x＜0）图象上一点，过点A作AB⊥y轴于点D，且D为线段AB的中点．若C为x轴上任意一点，且△ABC的面积为11，则k的值为（　　）
A．-
11
2
B．-11 C．11 D．
11
2
组卷：199引用：2难度：0.8
解析
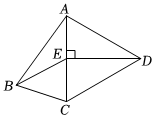9．如图，在四边形ABCD中，AB=AC=AD，∠BAD=90°，作DE⊥AC于点E，DE=8，连接BE，BE=BC，则AE的长为（　　）
A．10 B．8 C．6 D．4
组卷：247引用：6难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（满分60分）

27．某手机经销商计划同时购进甲乙两种型号手机，若购进2部甲型号手机和5部乙型号手机，共需要资金6000元；若购进3部甲型号手机和2部乙型号手机，共需要资金4600元．
（1）求甲、乙型号手机每部进价各为多少元；
（2）该店预计用不少于1.78万元且不多于1.92万元的资金购进这两种型号手机共20部，请问有多少种进货方案？
（3）若甲型号手机的售价为1500元，乙型号手机的售价为1450元，为了促销，公司决定每售出一台乙型号手机．返还顾客现金a元，甲型号手机售价不变，要使（2）中购进的手机全部售完，每种方案获利相同，求a的值．
组卷：81引用：5难度：0.5
解析
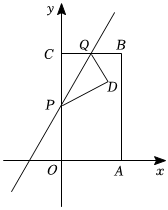28．如图，矩形OABC的顶点A，C分别在x轴和y轴上，OA，OC（OA＜OC）的长是一元二次方程
x
2
-
（
3
+
3
3
）
x
+
9
3
=
0
的两个实数根，点P从点C出发，以每秒
3
个单位长度的速度向终点O运动，同时点Q从点C出发，以每秒1个单位长度的速度向终点B运动，将△CPQ沿直线PQ折叠得到△DPQ，设△DPQ与矩形OABC重合部分的面积为S，运动时间为t秒．
（1）求点B的坐标；
（2）求S与t的函数关系式，并写出自变量的取值范围；
（3）当点D落在AB上时，点N在x轴上，直线PQ上是否存在点M，使以D，Q，M，N为顶点的四边形是平行四边形？若存在，直接出点M的坐标；若不存在，请说明理由．
组卷：45引用：3难度：0.3
解析