当前位置：试卷中心 > 试卷详情

2021-2022学年山东省泰安市新泰市七年级（下）期末数学试卷（五四学制）

发布：2025/11/19 1:0:7

一、选择题（本大题共12小题，在每小题给出的四个选项中，只有一个是正确的，请把正确的选项选出来，每小题选对得4分，选错、不选或选出的答案超过一个，均记零分）

1．有大小两种货车，2辆大货车与3辆小货车一次可以运货15.5吨，5辆大货车与6辆小货车一次可以运货35吨．设一辆大货车一次可以运货x吨，一辆小货车一次可以运货y吨，根据题意所列方程组正确的是（　　）
A．
2
x
+
3
y
=
15
.
5
5
x
+
6
y
=
35
B．
2
x
+
3
y
=
35
5
x
+
6
y
=
15
.
5
C．
3
x
+
2
y
=
15
.
5
5
x
+
6
y
=
35
D．
2
x
+
3
y
=
15
.
5
6
x
+
5
y
=
35
组卷：3198引用：58难度：0.7
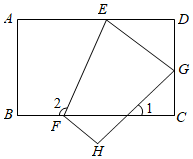2．如图，把一张长方形纸片ABCD沿EF折叠后，点A落在CD边上的点G处，点B落在点H处，若∠1=50°，则图中∠2的度数为（　　）
A．100° B．105° C．110° D．115°
组卷：875引用：4难度：0.7
3．如图，下列说法中错误的是（　　）
A．∠1不是三角形ABC的外角
B．∠B＜∠1+∠2
C．∠ACD是三角形ABC的外角
D．∠ACD＞∠A+∠B
组卷：238引用：8难度：0.9
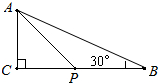4．如图，△ABC中，∠C=90°，AC=3，∠B=30°，点P是BC边上的动点，则AP长不可能是（　　）
A．3.5 B．4.2 C．5.8 D．7
组卷：2948引用：78难度：0.9
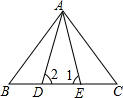5．如图，已知△ABE≌△ACD，∠1=∠2，∠B=∠C，不正确的等式是（　　）
A．AB=AC B．∠BAE=∠CAD C．BE=DC D．AD=DE
组卷：10395引用：192难度：0.9
6．不等式2-2x＞0的解集在数轴上表示正确的是（　　）
A． B．
C． D．
组卷：310引用：4难度：0.7
7．下列命题是假命题的是（　　）
A．四个角相等的四边形是矩形
B．对角线相等的平行四边形是矩形
C．对角线垂直的四边形是菱形
D．对角线垂直的平行四边形是菱形
组卷：1343引用：94难度：0.9
8．如图，在数轴上表示不等式组
x
＞
1
x
-
2
＞
0
的解集，其中正确的是（　　）
A． B． C． D．
组卷：432引用：10难度：0.9
9．下列方程是二元一次方程的是（　　）
A．-y+xy=2 B．3x-11=5x C．3x=2+y D．
2
x
-
6
y
=
1
2
组卷：1557引用：10难度：0.8
10．直角三角形的面积为S，斜边上的中线长为d,则这个三角形周长为（　　）
A．
d
2
+
S
+
2
d
B．
d
2
-
S
-
d
C．
2
d
2
+
S
+
2
d
D．
2
d
2
+
S
+
d
组卷：120引用：5难度：0.9
11．如图是一个可以自由转动的正六边形转盘，其中三个正三角形涂有阴影，转动指针，指针落在有阴影的区域内的概率为a,如果投掷一枚硬币，正面向上的概率为b,关于a、b大小的正确判断是（　　）
A．a＞b B．a=b C．a＜b D．不能判断
组卷：645引用：68难度：0.9
12．如图，BC⊥AE于点C，CD∥AB，∠1=35°，则∠B等于（　　）
A．35° B．45° C．55° D．65°
组卷：199引用：6难度：0.9

二、填空题（本大题共6小题，每小题4分，满分24分）

13．在△ABC中，将∠B、∠C按如图所示方式折叠，点B、C均落于边BC上一点G处，线段MN、EF为折痕．若∠A=82°，则∠MGE=
°．
组卷：1153引用：17难度：0.6
14．已知两个角的一边平行，另一边在同一直线上，其中一个角的度数是65°，则另一个角的度数是
．
组卷：12引用：2难度：0.8
15．如图是由四个直角边长分别为2和4的全等的直角三角形拼成的“赵爽弦图”飞镖板，小明站在投镖线上向飞镖板投掷飞镖（假设投掷的飞镖均扎在飞镖板上），则针扎在阴影部分的概率是
．
组卷：65引用：3难度：0.6
16．小明为全班六一儿童节的活动准备奖品，A奖品每个2元，B奖品每个7元，购买A奖品x个，B奖品y个，共76元．
（1）若x=10，则y=
；
（2）若同时购买两种奖品，则小明共有
种不同的选购方案．
组卷：105引用：2难度：0.5
17．如果关于x的不等式（a-1）x＜a+5和2x＜4的解集相同，则a的值为

．
组卷：661引用：29难度：0.5
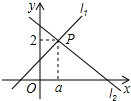18．直线l₁：y=x+1与直线l₂：y=mx+n相交于点P（a,2），则关于x的不等式x+1≥mx+n的解集为
．
组卷：5551引用：136难度：0.7

三、解答题（本大题共7小题，满分78分，解答应写出必要的文字说明、证明过程或推演步骤）

19．为提高饮水质量，越来越多的居民选购家用净水器．一商场抓住商机，从厂家购进了A、B两种型号家用净水器共160台，A型号家用净水器进价是150元/台，B型号家用净水器进价是350元/台，购进两种型号的家用净水器共用去36000元．
（1）求A、B两种型号家用净水器各购进了多少台；
（2）为使每台B型号家用净水器的毛利润是A型号的2倍，且保证售完这160台家用净水器的毛利润不低于11000元，求每台A型号家用净水器的售价至少是多少元．（注：毛利润=售价-进价）
组卷：6544引用：101难度：0.7
20．对于实数x,y我们定义一种新运算R（x,y）=ax+by（其中a,b均为非零常数），由这种运算得到的数我们称之为彩虹数，记为R（x,y），其中x,y叫做彩虹数的一个数对．若实数x,y都取正整数，我们称这样的彩虹数为正向彩虹数，这时的x,y叫做正向彩虹数的正向数对．
（1）若R（x,y）=2x+3y,则R（10，3）=
，R（
2
3
，-
3
2
）=
；
（2）已知R（3，-2）=5，R（
1
3
，
1
2
）=2，若正向彩虹数R（x,y）=62，求满足这样的正向彩虹数对有多少个．
组卷：121引用：1难度：0.5
21．阅读下面材料小明遇到这样一个问题：如图1，在△ABC中，∠B=2∠C，AD⊥BC于点D，求证：BC=AB+2BD．小明利用条件AD⊥BC在CD上截取DH=BD，如图2，连接AH既构造了等腰△ABH，又得到BH=2BD，从而命题得证．
（1）根据阅读材料证明BC=AB+2BD；
（2）参考小明的方法解决下面的问题；如图3在△ABC中，∠BAC=90°，∠ABD=∠BCE，∠ABC=∠DCE，请探究AD与BE的数量关系，并说明理由．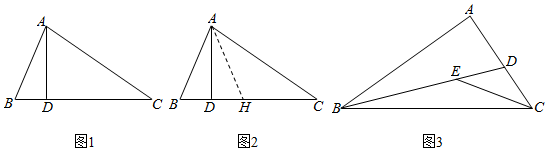
组卷：1553引用：6难度：0.4
22．（1）计算：
|
3
-
2
|
+
3
-
8
+
（
-
2
）
2
-
|
-
2
|

（2）解方程组
x
=
2
y
-
1
3
x
+
y
=
4

（3）解不等式组
4
（
x
+
1
）
＜
7
x
+
13
x
-
4
＜
x
-
8
3
，并写出它所有负整数解．
组卷：431引用：1难度：0.5
23．已知，如图，BCE、AFE是直线，AB∥CD，AD∥BE，∠1=∠2．求证：∠3=∠4．

组卷：62引用：1难度：0.5
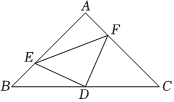24．已知：三角形ABC中，∠A=90°，AB=AC，D为BC的中点，如图，E，F分别是AB，AC上的点，且BE=AF，求证：△DEF为等腰直角三角形．
组卷：2872引用：5难度：0.1

25．为倡导“全民健身，健康向上”的生活方式，我市教育系统特举办教职工气排球比赛．比赛采取小组循环，每场比赛实行三局两胜制，取实力最强的两支队伍参加决赛，从C组的比分胜负表中知道二中胜4场负1场．
教职工气排球比赛比分胜负表

C组一中二中三中四中五中六中

一中 \ 21：16 21：19 21：9 22：24 15：21

14：21 24：22 21：23 5：21 18：21

12：15 15：9

二中 16：21 \ 21：13 21：13 14：21 22：20

21：14 21：17 21：11 19：21 19：21

15：12 16：14

三中 19：21 13：21 \ 21：16 21：18 B′

22：24 17：21 21：18 6：21

12：15

四中 9：21 13：21 16：21 \ A′ 21：11

23：21 11：21 18：21 9：21

9：15 8：15

五中 24：22 21：14 18：21 A \ 21：23

21：5 21：19 21：6 18：21

15：12

六中 21：15 20：22 B 11：21 23：21 \

21：18 21：19 21：9 21：18

14：16 15：8

（1）根据表中数据可知，一中共获胜
场，“四中VS五中”的比赛获胜可能性最大的是
；
（2）若A处的比分是21：10和21：8，并且参加决赛的队伍是二中和五中，则B′处的比分可以是
和
（两局结束比赛，根据自己的理解填写比分）；
（3）若A′处的比分是10：21和8：21，B处的比分是21：18，15：21，15：12，那么实力最强的是哪两支队伍，请说明理由．

组卷：600引用：9难度：0.3

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

C组	一中	二中	三中	四中	五中	六中
一中	\	21：16	21：19	21：9	22：24	15：21
		14：21	24：22	21：23	5：21	18：21
		12：15		15：9
二中	16：21	\	21：13	21：13	14：21	22：20
	21：14		21：17	21：11	19：21	19：21
	15：12					16：14
三中	19：21	13：21	\	21：16	21：18	B′
	22：24	17：21		21：18	6：21
					12：15
四中	9：21	13：21	16：21	\	A′	21：11
	23：21	11：21	18：21			9：21
	9：15					8：15
五中	24：22	21：14	18：21	A	\	21：23
	21：5	21：19	21：6			18：21
			15：12
六中	21：15	20：22	B	11：21	23：21	\
	21：18	21：19		21：9	21：18
		14：16		15：8

A．	B．
C．	D．

2021-2022学年山东省泰安市新泰市七年级（下）期末数学试卷（五四学制）

一、选择题（本大题共12小题，在每小题给出的四个选项中，只有一个是正确的，请把正确的选项选出来，每小题选对得4分，选错、不选或选出的答案超过一个，均记零分）

1．有大小两种货车，2辆大货车与3辆小货车一次可以运货15.5吨，5辆大货车与6辆小货车一次可以运货35吨．设一辆大货车一次可以运货x吨，一辆小货车一次可以运货y吨，根据题意所列方程组正确的是（ ）

2．如图，把一张长方形纸片ABCD沿EF折叠后，点A落在CD边上的点G处，点B落在点H处，若∠1=50°，则图中∠2的度数为（ ）

3．如图，下列说法中错误的是（ ）

4．如图，△ABC中，∠C=90°，AC=3，∠B=30°，点P是BC边上的动点，则AP长不可能是（ ）

5．如图，已知△ABE≌△ACD，∠1=∠2，∠B=∠C，不正确的等式是（ ）

6．不等式2-2x＞0的解集在数轴上表示正确的是（ ）

7．下列命题是假命题的是（ ）

8．如图，在数轴上表示不等式组x＞1x-2＞0的解集，其中正确的是（ ）

9．下列方程是二元一次方程的是（ ）

10．直角三角形的面积为S，斜边上的中线长为d,则这个三角形周长为（ ）

11．如图是一个可以自由转动的正六边形转盘，其中三个正三角形涂有阴影，转动指针，指针落在有阴影的区域内的概率为a,如果投掷一枚硬币，正面向上的概率为b,关于a、b大小的正确判断是（ ）

12．如图，BC⊥AE于点C，CD∥AB，∠1=35°，则∠B等于（ ）

二、填空题（本大题共6小题，每小题4分，满分24分）

13．在△ABC中，将∠B、∠C按如图所示方式折叠，点B、C均落于边BC上一点G处，线段MN、EF为折痕．若∠A=82°，则∠MGE=°．

14．已知两个角的一边平行，另一边在同一直线上，其中一个角的度数是65°，则另一个角的度数是 ．

15．如图是由四个直角边长分别为2和4的全等的直角三角形拼成的“赵爽弦图”飞镖板，小明站在投镖线上向飞镖板投掷飞镖（假设投掷的飞镖均扎在飞镖板上），则针扎在阴影部分的概率是 ．

16．小明为全班六一儿童节的活动准备奖品，A奖品每个2元，B奖品每个7元，购买A奖品x个，B奖品y个，共76元．（1）若x=10，则y=；（2）若同时购买两种奖品，则小明共有 种不同的选购方案．

17．如果关于x的不等式（a-1）x＜a+5和2x＜4的解集相同，则a的值为 ．

18．直线l1：y=x+1与直线l2：y=mx+n相交于点P（a,2），则关于x的不等式x+1≥mx+n的解集为 ．

三、解答题（本大题共7小题，满分78分，解答应写出必要的文字说明、证明过程或推演步骤）

22．（1）计算：|3-2|+3-8+（-2）2-|-2|（2）解方程组x=2y-13x+y=4（3）解不等式组4（x+1）＜7x+13x-4＜x-83，并写出它所有负整数解．

23．已知，如图，BCE、AFE是直线，AB∥CD，AD∥BE，∠1=∠2．求证：∠3=∠4．​​

24．已知：三角形ABC中，∠A=90°，AB=AC，D为BC的中点，如图，E，F分别是AB，AC上的点，且BE=AF，求证：△DEF为等腰直角三角形．

1．有大小两种货车，2辆大货车与3辆小货车一次可以运货15.5吨，5辆大货车与6辆小货车一次可以运货35吨．设一辆大货车一次可以运货x吨，一辆小货车一次可以运货y吨，根据题意所列方程组正确的是（　　）

2．如图，把一张长方形纸片ABCD沿EF折叠后，点A落在CD边上的点G处，点B落在点H处，若∠1=50°，则图中∠2的度数为（　　）

3．如图，下列说法中错误的是（　　）

4．如图，△ABC中，∠C=90°，AC=3，∠B=30°，点P是BC边上的动点，则AP长不可能是（　　）

5．如图，已知△ABE≌△ACD，∠1=∠2，∠B=∠C，不正确的等式是（　　）

6．不等式2-2x＞0的解集在数轴上表示正确的是（　　）

7．下列命题是假命题的是（　　）

8．如图，在数轴上表示不等式组
x
＞
1
x
-
2
＞
0
的解集，其中正确的是（　　）

9．下列方程是二元一次方程的是（　　）

10．直角三角形的面积为S，斜边上的中线长为d,则这个三角形周长为（　　）

11．如图是一个可以自由转动的正六边形转盘，其中三个正三角形涂有阴影，转动指针，指针落在有阴影的区域内的概率为a,如果投掷一枚硬币，正面向上的概率为b,关于a、b大小的正确判断是（　　）

12．如图，BC⊥AE于点C，CD∥AB，∠1=35°，则∠B等于（　　）

13．在△ABC中，将∠B、∠C按如图所示方式折叠，点B、C均落于边BC上一点G处，线段MN、EF为折痕．若∠A=82°，则∠MGE=
°．

14．已知两个角的一边平行，另一边在同一直线上，其中一个角的度数是65°，则另一个角的度数是
．

15．如图是由四个直角边长分别为2和4的全等的直角三角形拼成的“赵爽弦图”飞镖板，小明站在投镖线上向飞镖板投掷飞镖（假设投掷的飞镖均扎在飞镖板上），则针扎在阴影部分的概率是
．

16．小明为全班六一儿童节的活动准备奖品，A奖品每个2元，B奖品每个7元，购买A奖品x个，B奖品y个，共76元．
（1）若x=10，则y=
；
（2）若同时购买两种奖品，则小明共有
种不同的选购方案．

17．如果关于x的不等式（a-1）x＜a+5和2x＜4的解集相同，则a的值为

．

18．直线l₁：y=x+1与直线l₂：y=mx+n相交于点P（a,2），则关于x的不等式x+1≥mx+n的解集为
．

22．（1）计算：
|
3
-
2
|
+
3
-
8
+
（
-
2
）
2
-
|
-
2
|

（2）解方程组
x
=
2
y
-
1
3
x
+
y
=
4

（3）解不等式组
4
（
x
+
1
）
＜
7
x
+
13
x
-
4
＜
x
-
8
3
，并写出它所有负整数解．

23．已知，如图，BCE、AFE是直线，AB∥CD，AD∥BE，∠1=∠2．求证：∠3=∠4．